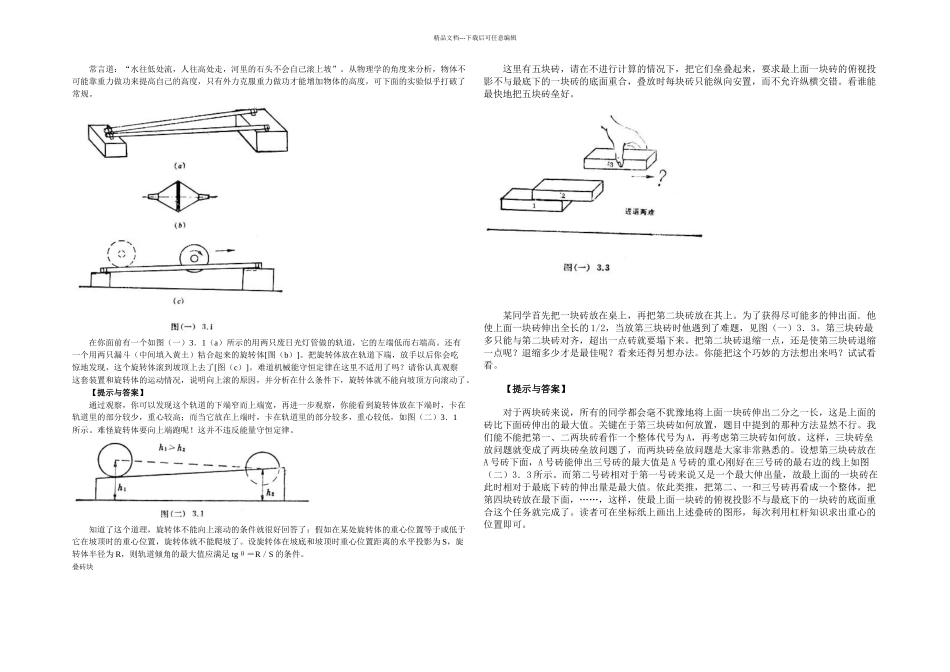
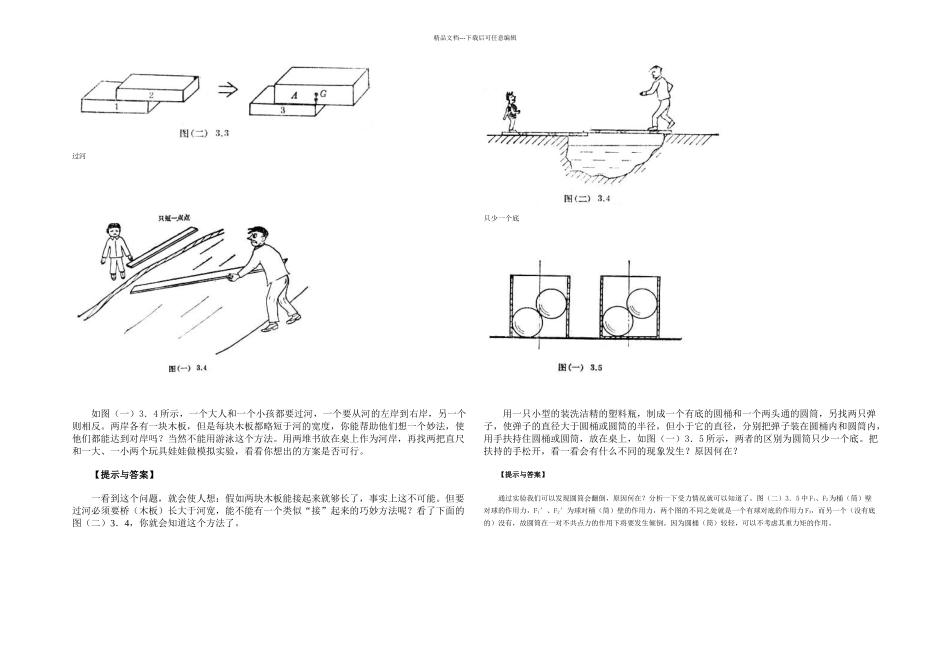
精品文档---下载后可任意编辑 常言道:“水往低处流,人往高处走,河里的石头不会自己滚上坡”。从物理学的角度来分析,物体不可能靠重力做功来提高自己的高度,只有外力克服重力做功才能增加物体的高度,可下面的实验似乎打破了常规。 在你面前有一个如图(一)3.1(a)所示的用两只废日光灯管做的轨道,它的左端低而右端高。还有一个用两只漏斗(中间填入黄土)粘合起来的旋转体[图(b)]。把旋转体放在轨道下端,放手以后你会吃惊地发现,这个旋转体滚到坡顶上去了[图(c)]。难道机械能守恒定律在这里不适用了吗?请你认真观察这套装置和旋转体的运动情况,说明向上滚的原因,并分析在什么条件下,旋转体就不能向坡顶方向滚动了。 【提示与答案】 通过观察,你可以发现这个轨道的下端窄而上端宽,再进一步观察,你能看到旋转体放在下端时,卡在轨道里的部分较少,重心较高;而当它放在上端时,卡在轨道里的部分较多,重心较低,如图(二)3.1所示。难怪旋转体要向上端跑呢!这并不违反能量守恒定律。 知道了这个道理,旋转体不能向上滚动的条件就很好回答了:假如在某处旋转体的重心位置等于或低于它在坡顶时的重心位置,旋转体就不能爬坡了。设旋转体在坡底和坡顶时重心位置距离的水平投影为 S,旋转体半径为 R,则轨道倾角的最大值应满足 tgθ=R/S 的条件。叠砖块 这里有五块砖,请在不进行计算的情况下,把它们垒叠起来,要求最上面一块砖的俯视投影不与最底下的一块砖的底面重合,叠放时每块砖只能纵向安置,而不允许纵横交错。看谁能最快地把五块砖垒好。 某同学首先把一块砖放在桌上,再把第二块砖放在其上。为了获得尽可能多的伸出面.他使上面一块砖伸出全长的 1/2,当放第三块砖时他遇到了难题,见图(一)3.3。第三块砖最多只能与第二块砖对齐,超出一点砖就要塌下来。把第二块砖退缩一点,还是使第三块砖退缩一点呢?退缩多少才是最佳呢?看来还得另想办法。你能把这个巧妙的方法想出来吗?试试看看。 【提示与答案】 对于两块砖来说,所有的同学都会毫不犹豫地将上面一块砖伸出二分之一长,这是上面的砖比下面砖伸出的最大值。关键在于第三块砖如何放置,题目中提到的那种方法显然不行。我们能不能把第一、二两块砖看作一个整体代号为 A,再考虑第三块砖如何放。这样,三块砖垒放问题就变成了两块砖垒放问题了,而两块砖垒放问题是大家非常熟悉的。设想第三块砖放在A 号砖下面,A 号砖能伸出三号砖的最大值...