机械工程控制基础课后习题

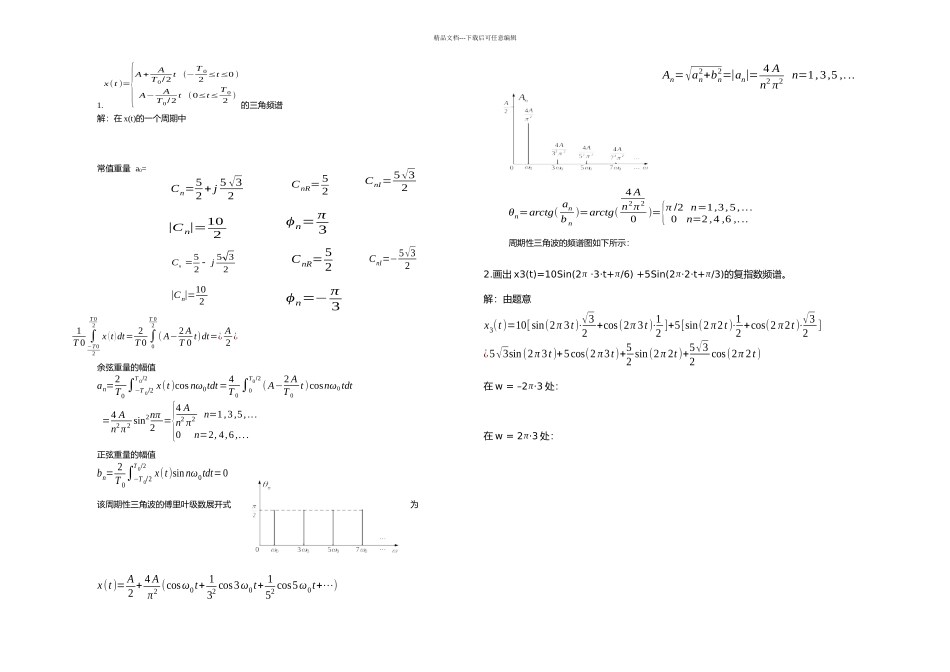
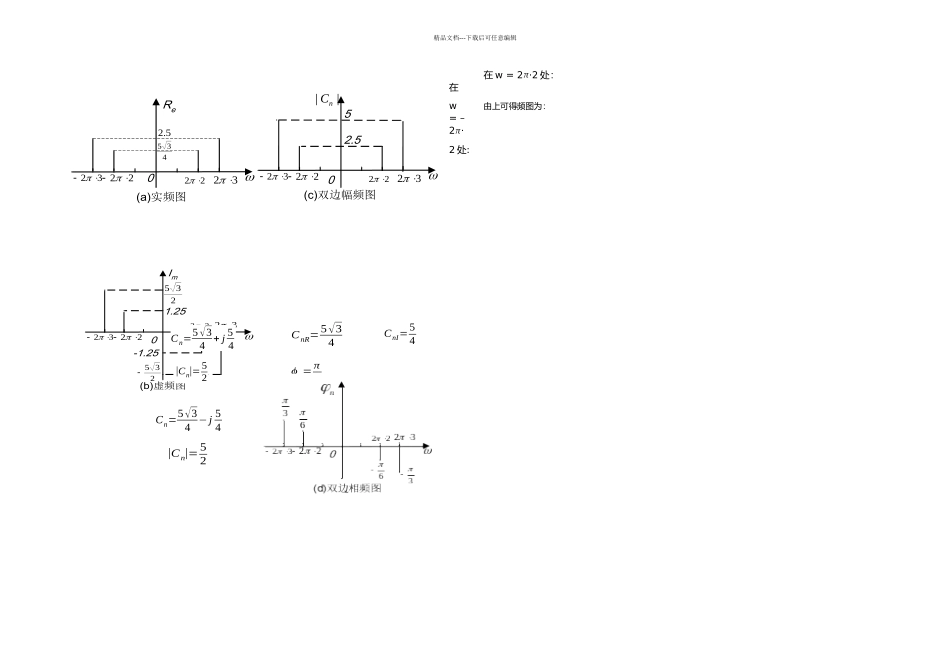
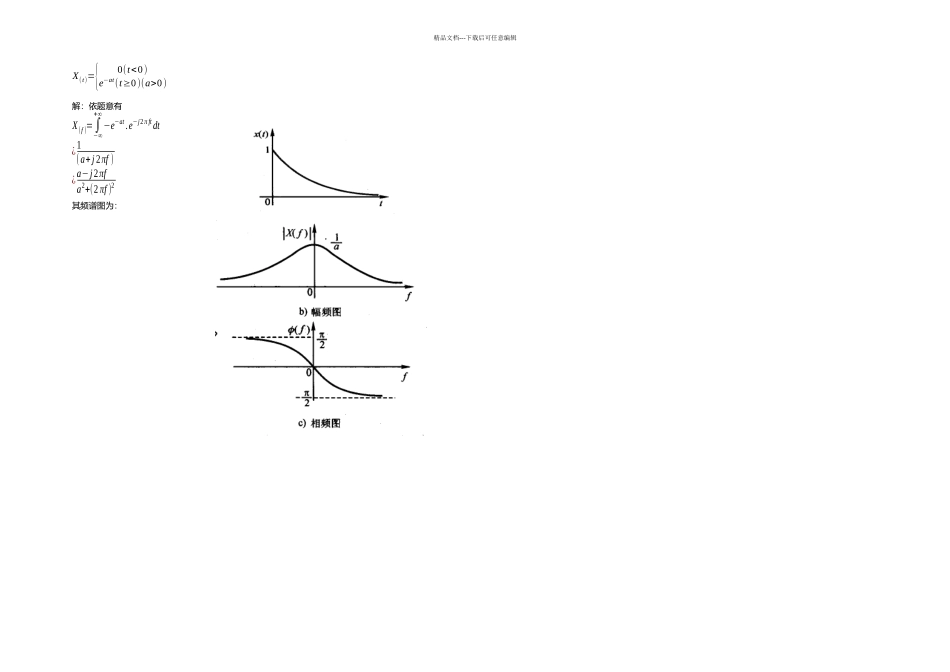
精品文档---下载后可任意编辑1.x(t )={A +AT0/2 t (− T 02 ≤t≤0)A−AT0/2 t (0≤t≤ T 02 )的三角频谱解：在 x(t)的一个周期中常值重量 a0= 1T 0 ∫−T 02T 02x (t)dt= 2T 0 ∫0T 02( A−2 AT 0 t)dt=¿ A2 ¿余弦重量的幅值an=2T0 ∫−T 0/2T 0/2x(t )cos nω0tdt=4T 0 ∫0T0/2( A−2 AT 0t )cosnω0tdt=4 An2π 2 sin2nπ2={4 An2 π2n=1,3,5,...0n=2, 4,6,...正弦重量的幅值bn= 2T 0∫−T 0/2T 0/2x(t )sinnω0tdt=0该周期性三角波的傅里叶级数展开式为x(t )= A2 + 4 Aπ2 (cosω0t+ 132 cos3ω0t+ 152 cos5ω0t+⋯)An=√an2+bn2=|an|= 4 An2 π2 n=1,3,5 ,...θn=arctg( anb n)=arctg(4 An2π 20)={π /2 n=1,3,5,...0n=2,4 ,6 ,...周期性三角波的频谱图如下所示：2.画出 x3(t)=10Sin(2π ·3·t+π/6) +5Sin(2π·2·t+π/3)的复指数频谱。解：由题意x3(t )=10[sin(2π 3t )⋅√32+cos(2π 3t )⋅12 ]+5[sin(2 π2t )⋅12 +cos(2 π2t )⋅√32]¿5√3sin(2π 3t )+5cos(2 π3t )+52 sin(2π 2t )+5√32cos(2π 2t )在 w = –2π·3 处：在 w = 2π·3 处：23525jCnCnI= 5√32CnR= 52Cn=52 + j 5 √32|C n|=102ϕn= π3CnR= 52CnI=−5√32|Cn|=102ϕn=− π3精品文档---下载后可任意编辑在w = –2π·2 处:在 w = 2π·2 处：由上可得频图为：Re022 32 22 32 (a)实频图5.2435022 32 22 32 2.55||nC(c)双边幅频图Im0223222321.25(b)虚频图-1.25235235Cn=5√34 + j 54CnR= 5√34CnI=54ϕn= π6|Cn|=52CnI=−54CnR=5√34Cn=5√34 −j 54ϕn=− π6|Cn|= 52精品文档---下载后可任意编辑X(t)={0(t<0)e−at(t≥0)(a>0)解：依题意有X(f )=∫−∞+∞−e−at.e−j2π ftdt¿1(a+j2πf )¿a−j2πfa2+(2 πf )2其频谱图为：精品文档---下载后可任意编辑x(t )={cosω0t |t|T 0解：w(t)为窗函数W(f) = 2Tsinc (2πTf 0)x(t) = w(t) cos(2πTf 0)cos(2πTf 0) = 12(e−j2π f 0t+ej2π f 0t)x(t) = w(t) 12(e−j2π f 0t+ej2π f 0t) = 12 w (f −f 0)+ 12 w (f +f 0) = Tsinc [12 w (f −f 0)] + Tsinc [12 w (f +f 0)]画出频谱图：