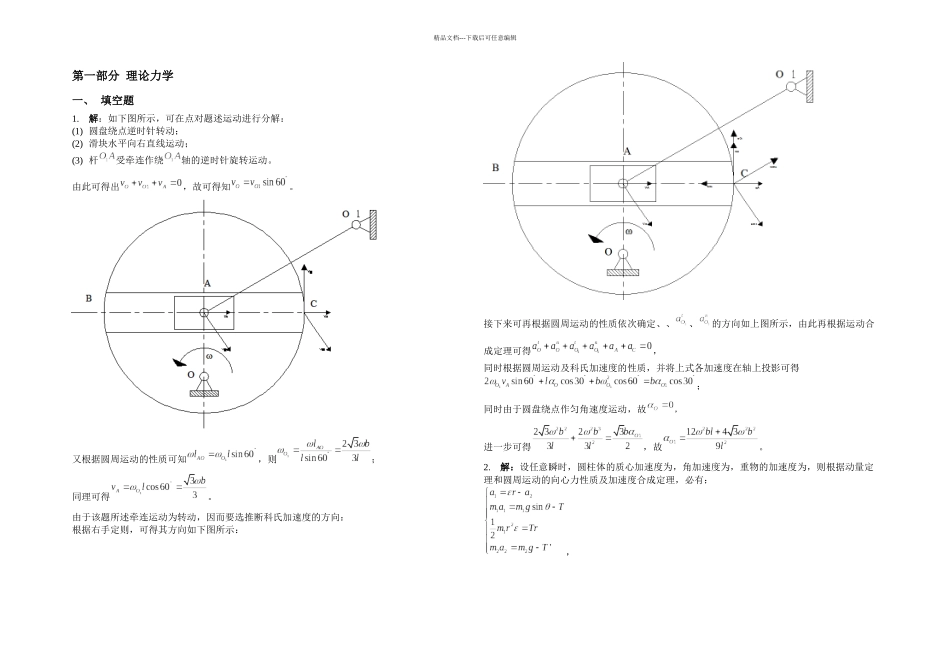
精品文档---下载后可任意编辑第一部分 理论力学一、 填空题1.解:如下图所示,可在点对题述运动进行分解:(1) 圆盘绕点逆时针转动;(2) 滑块水平向右直线运动;(3) 杆受牵连作绕轴的逆时针旋转运动。由此可得出,故可得知。又根据圆周运动的性质可知,则;同理可得。由于该题所述牵连运动为转动,因而要选推断科氏加速度的方向:根据右手定则,可得其方向如下图所示:接下来可再根据圆周运动的性质依次确定、、、的方向如上图所示,由此再根据运动合成定理可得,同时根据圆周运动及科氏加速度的性质,并将上式各加速度在轴上投影可得;同时由于圆盘绕点作匀角速度运动,故,进一步可得,故。2.解:设任意瞬时,圆柱体的质心加速度为,角加速度为,重物的加速度为,则根据动量定理和圆周运动的向心力性质及加速度合成定理,必有:,精品文档---下载后可任意编辑联立,可解得。3.解:由题意可得如下图所示的受力分析图(其中、分别代表滑动与滚动摩擦力,代表滚动阻力偶):由上图可知;由滚动阻碍定律可得;由此根据力偶的性质可得;同时根据滑动摩擦的性质;由于使得系统发生运动的力为,又由于,故可得。4.解:由题意可绘制如下图所示的运行与受力分析:首先,求解质心的位置:;刚体作定轴转动,初瞬时,应用动量矩定理得;又,由此得,故,因此;由质心运动定理:;故。又刚体与要保持动平衡,由此可得。5.解:⑴设物块下降距离时,速度为,则系统动能为:精品文档---下载后可任意编辑,其中:;;;;则;重力的功为:;应用动能定理并求导:;故。(2)如下图应用相对速度瞬心的动量矩定理:;其中,则可得。6.解:对图示机构进行受力分析,如下图所示。由图示可知,,,即,进而可推得,即;由摩擦力的公式可知,,由此可推得,由题意,,精品文档---下载后可任意编辑可推得。由刚体动力学静平衡条件可得,即,又,故可推得,同时,由题意可知,则故可推得,即。7.解:选定杆与及、滑块组成的系统为讨论对象,根据题意可绘制出如下图所示的受力分析:则该系统有 5个活动部件,存在 5 个旋转副、2 个移动副,故其自由度为个自由度;因此可选择为广义坐标,利用解析法求解:通过主动力偶、滑块的驱动力作用点处相应坐标、的变分,确定点铅垂方向和点水平方向的虚位移:,,虚功之和为,根据虚位移原理得,即。8.解:根据题意可做出如下图所示的断绳后的受力分析:由该图我们可以看出在断绳前,其重心为点,但在断绳后其重心迁移至点。由...