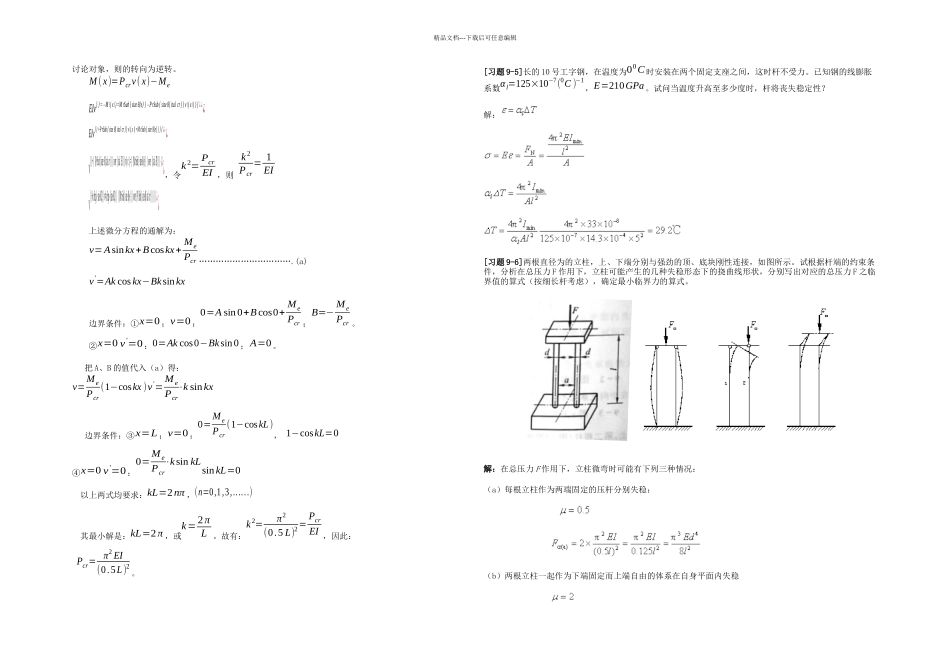
精品文档---下载后可任意编辑[习题 9-1]在§9-2 中已对两端球形铰支的等截面细长压杆,按图 a 所示坐标系及挠度曲线形状,导出了临界应力公式Pcr=π 2 EIl2。试分析当分别取图 b,c,d 所示坐标系及挠曲线形状时,压杆在作用下的挠曲线微分方程是否与图 a 情况下的相同,由此所得公式又是否相同。解:挠曲线微分方程与坐标系的 y 轴正向规定有关,与挠曲线的位置无关。因为(b)图与(a)图具有相同的坐标系,所以它们的挠曲线微分方程相同,都是EIw} } = - M \( x \) } { ¿¿¿。(c)、(d)的坐标系相同,它们具有相同的挠曲线微分方程:EIw} } =M \( x \) } {¿¿¿,显然,这微分方程与(a)的微分方程不同。临界力只与压杆的抗弯刚度、长度与两端的支承情况有关,与坐标系的选取、挠曲线的位置等因素无关。因此,以上四种情形的临界力具有相同的公式,即:Pcr=π 2 EIl2。[习题 9-2] 图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图 f 所示杆在中间支承处不能转动)?解:压杆能承受的临界压力为:Pcr= π2 EI( μ.l )2。由这公式可知,对于材料和截面相同的压杆,它们能承受的压力与原压相的相当长度的平方成反比,其中,为与约束情况有关的长度系数。(a)μl=1×5=5m(b)μl=0.7×7=4.9m(c)μl=0.5×9=4.5m(d)μl=2×2=4 m(e)μl=1×8=8m(f)μl=0.7×5=3.5m (下段);μl=0.5×5=2.5m(上段)故图 e 所示杆最小,图 f 所示杆最大。[习题 9-3] 图 a,b 所示的两细长杆均与基础刚性连接,但第一根杆(图 a)的基础放在弹性地基上,第二根杆(图 b)的基础放在刚性地基上。试问两杆的临界力是否均为Pcr=π 2 EImin(2.l )2?为什么?并由此推断压杆长因数是否可能大于 2。 螺旋千斤顶(图 c)的底座对丝杆(起顶杆)的稳定性有无影响?校核丝杆稳定性时,把它看作下端固定(固定于底座上)、上端自由、长度为的压杆是否偏于安全?精品文档---下载后可任意编辑解:临界力与压杆两端的支承情况有关。因为(a)的下支座不同于(b)的下支座,所以它们的临界力计算公式不同。(b)为一端固定,一端自由的情况,它的长度因素μ=2,其临界力为:Pcr=π 2 EImin(2.l )2。但是,(a)为一端弹簧支座,一端自由的情况,它的长度因素μ≠2,因此,不能用Pcr=π 2 EImin(2.l )2来计算临界力。 为了考察(a)情况下的临界力,我们不妨设下支座(B)的转动刚度C= Mϕ...