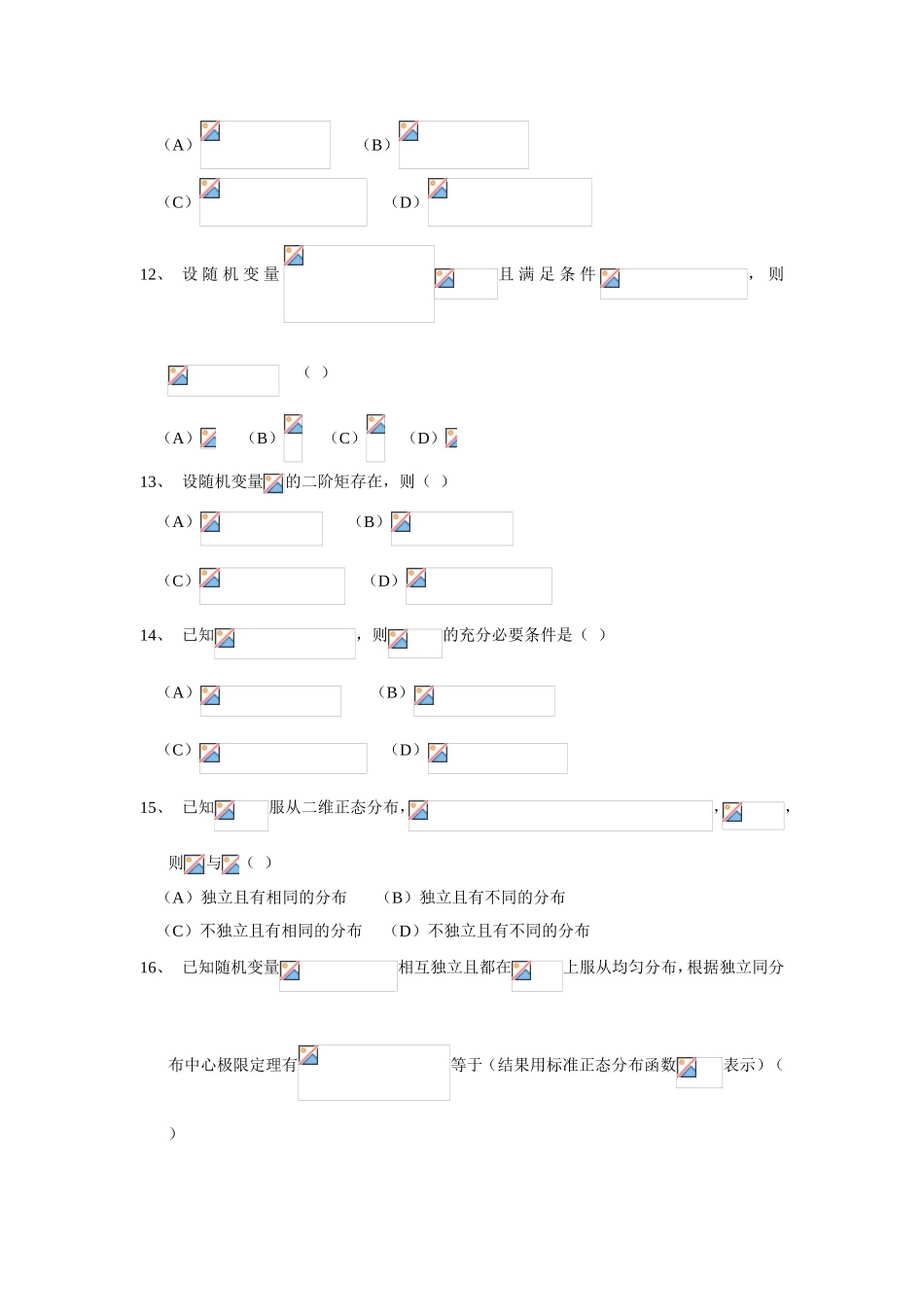
一、选择题1、设随机变量,事件,则()(A)与互不相容(B)包含(C)与对立(D)与相互独立2、已知为随机事件,,,则充要条件是()(A)(B)(C)(D)3、设为随机事件,,,则相互独立的充要条件是()(A)(B)(C)(D)4、设为随机事件,,则()(A)(B)(C)(D)5、设是离散型随机变量,(n为自然数,),则下列能成为X的概率分布的是()(A)(B)(C)(D)6、假设随机变量X的密度函数是偶函数,其分布函数是,则()(A)是偶函数(B)是奇函数(C)(D)7、假设随机变量X的分布函数为,概率密度函数,其中是正态分布的密度函数,是参数为的指数分布的密度函数,已知,,则()(A)(B)(C)(D)8、设随机变量X服从正态分布,其分布函数为,则对任意实数,有()(A)(B)(C)(D)9、假设一个设备在任何长为的时间内发生故障次数服从参数为的泊松分布,,表示相继两次故障之间时间的间隔,则对任意,概率等于()(A)(B)(C)(D)10、已知随机变量与相互独立且都服从正态分布,如果,则等于()(A)(B)(C)(D)11、设随机变量与相互独立且都服从正态分布,则()(A)(B)(C)(D)12、设随机变量且满足条件,则()(A)(B)(C)(D)13、设随机变量的二阶矩存在,则()(A)(B)(C)(D)14、已知,则的充分必要条件是()(A)(B)(C)(D)15、已知服从二维正态分布,,,则与()(A)独立且有相同的分布(B)独立且有不同的分布(C)不独立且有相同的分布(D)不独立且有不同的分布16、已知随机变量相互独立且都在上服从均匀分布,根据独立同分布中心极限定理有等于(结果用标准正态分布函数表示)()(A)(B)(C)(D)17、设总体其中已知,未知,为来自总体的简单随机样本,则下列表达式中不是统计量的是()(A)(B)(C)(D)18、设总体,分别为容量是的样本的均值和方差,则服从自由度为的t分布的随机变量是()(A)(B)(C)(D)19、假设是来自正态总体的简单随机样本,则()(A)(B)(C)(D)20、设总体,与相互独立,和分别来自总体和的两个样本,和分别为两个样本的方差,则()(A)(B)(C)(D)21、总体均值置信度为的置信区间为,其含意是()(A)总体均值的真值以的概率落入区间(B)样本均值以的概率落入区间(C)区间含总体均值的真值的概率为(D)区间含样本均值的概率为22、设总体,其中已知,则总体均值的置信区间长度与置信度的关系是()(A)当减小时,变小(B)当减小时,增大(C)当减小时,不变(D)当减小时,增减不定二、填空题1、设两个相互独立事件与至少有一个发生的概率为,发生不发生与发生不发生的概率相等,则_____2、从标号为的卡片中有放回的取三张(每次取一张,然后放回),则三个数中最大数为4的概率为_____3、在区间中随机地取出两个数,则“两数之积小于”的概率为_____4、已知,,与相互独立,如果,则_____5、某种产品由自动生产线进行生产,一旦出现不合格品就立即对其进行调整,经过调整后生产出的产品为不合格品的概率为0.1,那么两次调整之间至少生产3件产品的概率为_____6、设随机变量的概率密度函数为,以表示对进行三次独立重复观察中事件出现的次数,则_____7、设二维随机变量(,)的概率密度为,则_____8、已知离散随机变量的分布律为:,则随机变量的数学期望为_____9、已知一批零件的长度(单位:cm)服从,从中随机的抽取16个零件,得到长度的平均值为40(cm),则的置信度为0.95的置信区间为10、设总体的概率密度函数为,而是来自总体的简单随机样本,则未知参数的矩估计量为_____三、计算题1、某装置的平均工作温度据制造厂家称低于,今从一个由16台装置构成的随机样本测得工作温度得平均值和标准差分别为和,根据这些数据能否支持厂家结论?设,并假定工作温度近似服从正态分布。2、假设批量生产的某种配件的内径,今随机抽取16个配件,测得平均内径毫米,样本标准差毫米,求的90%的置信区间。3、设,为简单随机样本,求的极大似然估计量。4、设从总体,中分别抽取容量为的独立样本,计算得(1)若已知求得置信度为95%置信区间。(2)若已知求得置信度...