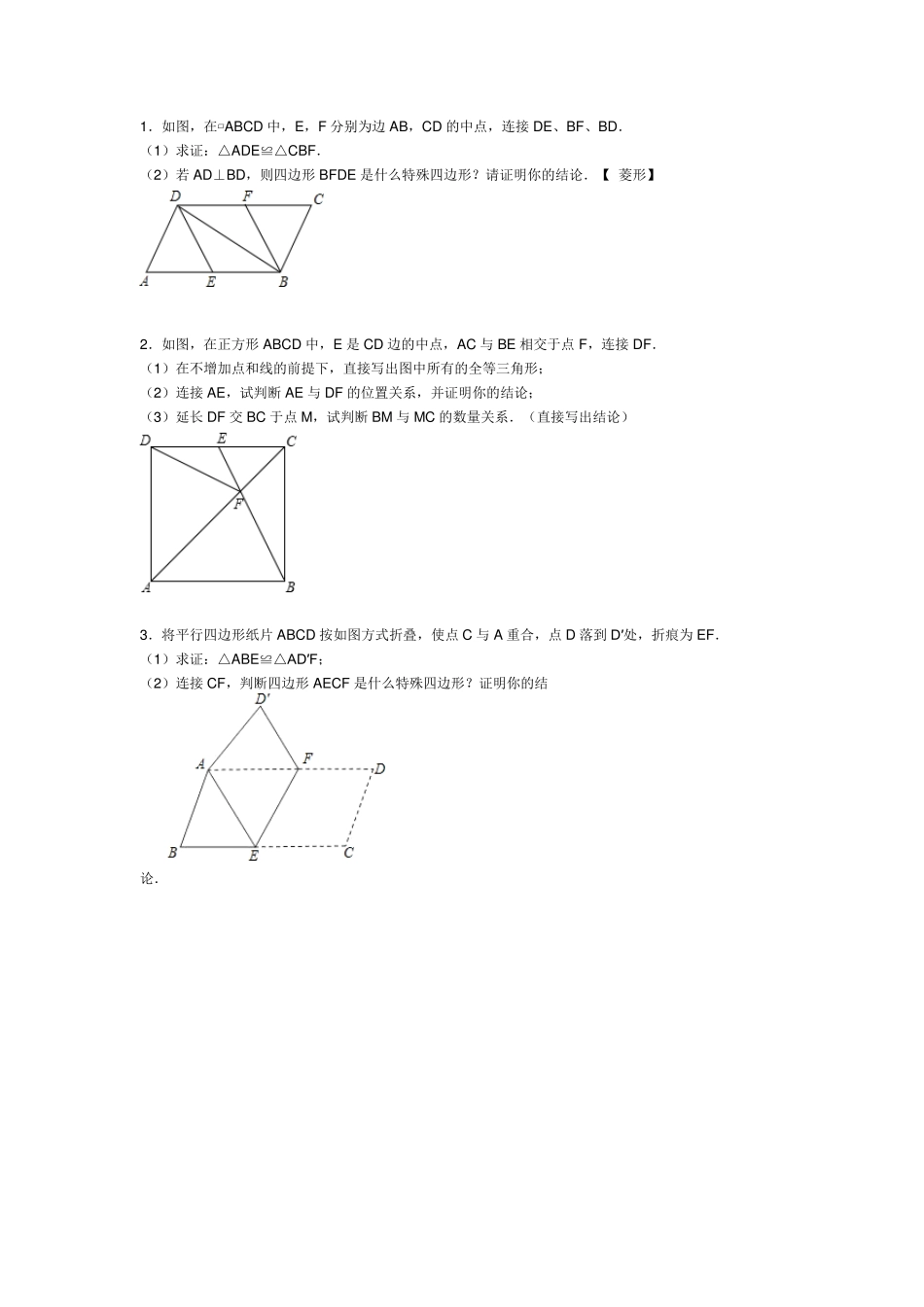
1.如图,在▱ ABCD 中,E,F 分别为边AB,CD 的中点,连接DE、BF、BD. (1)求证:△ADE≌△CBF. (2)若 AD⊥BD,则四边形 BFDE 是什么特殊四边形?请证明你的结论.【 菱形】 2.如图,在正方形 ABCD 中,E 是 CD 边的中点,AC 与 BE 相交于点F,连接DF. (1)在不增加点和线的前提下,直接写出图中所有的全等三角形; (2)连接AE,试判断 AE 与 DF 的位置关系,并证明你的结论; (3)延长 DF 交 BC 于点M ,试判断 BM 与 M C 的数量关系.(直接写出结论) 3.将平行四边形纸片 ABCD 按如图方式折叠,使点C 与 A 重合,点D 落到 D′处,折痕为EF. (1)求证:△ABE≌△AD′F; (2)连接CF,判断四边形 AECF 是什么特殊四边形?证明你的结论. 4.如图所示,∠ADB=∠ADC,BD=CD. (1)求证:△ABD≌△ACD; (2)设 E 是 AD 延长线上的动点,当点 E 移动到什么位置时,四边形 ACEB 为菱形?说明你的理由. 5.如图,在等边△ABC 中,点 D 为 AC 中点,以 AD 为边作菱形 ADEF,且 AF∥BC,连接 FC 交 DE 于点 G . (1)求证:△ADB≌△AFC; (2)写出图中除(1)以外的两对全等三角形(不要求写证明过程). 6.如图,四边形ABCD 是矩形,O 是它的中心,E、F 是对角线AC 上的点. (1)如果 ,则△DEC≌△BFA(请你填上能使结论成立的一个条件); (2)证明你的结论. 7.(1)如图1,在正方形ABCD 中,M 是BC 边(不含端点B、C)上任意一点,P 是BC 延长线上一点,N 是∠DCP 的平分线上一点.若∠AMN=90°,求证:AM=MN. 下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明. 证明:在边AB 上截取 AE=MC,连接 ME.正方形ABCD 中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE. (下面请你完成余下的证明过程) (2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N 是∠ACP 的平分线上一点,则∠AMN=60°时,结论AM=MN 是否还成立?请说明理由. (3)若将(1)中的“正方形ABCD”改为“正n 边形ABCD… X,请你作出猜想:当∠AMN= 时,结论AM=MN 仍然成立.(直接写出答案,不需要证明) 8.如图,四边形ABCD 是边长为a 的正方形,点G,E 分别是边AB,BC 的中点,∠AEF=90°,且 EF 交正方形外角的平分线 CF 于点F. (1)证明...