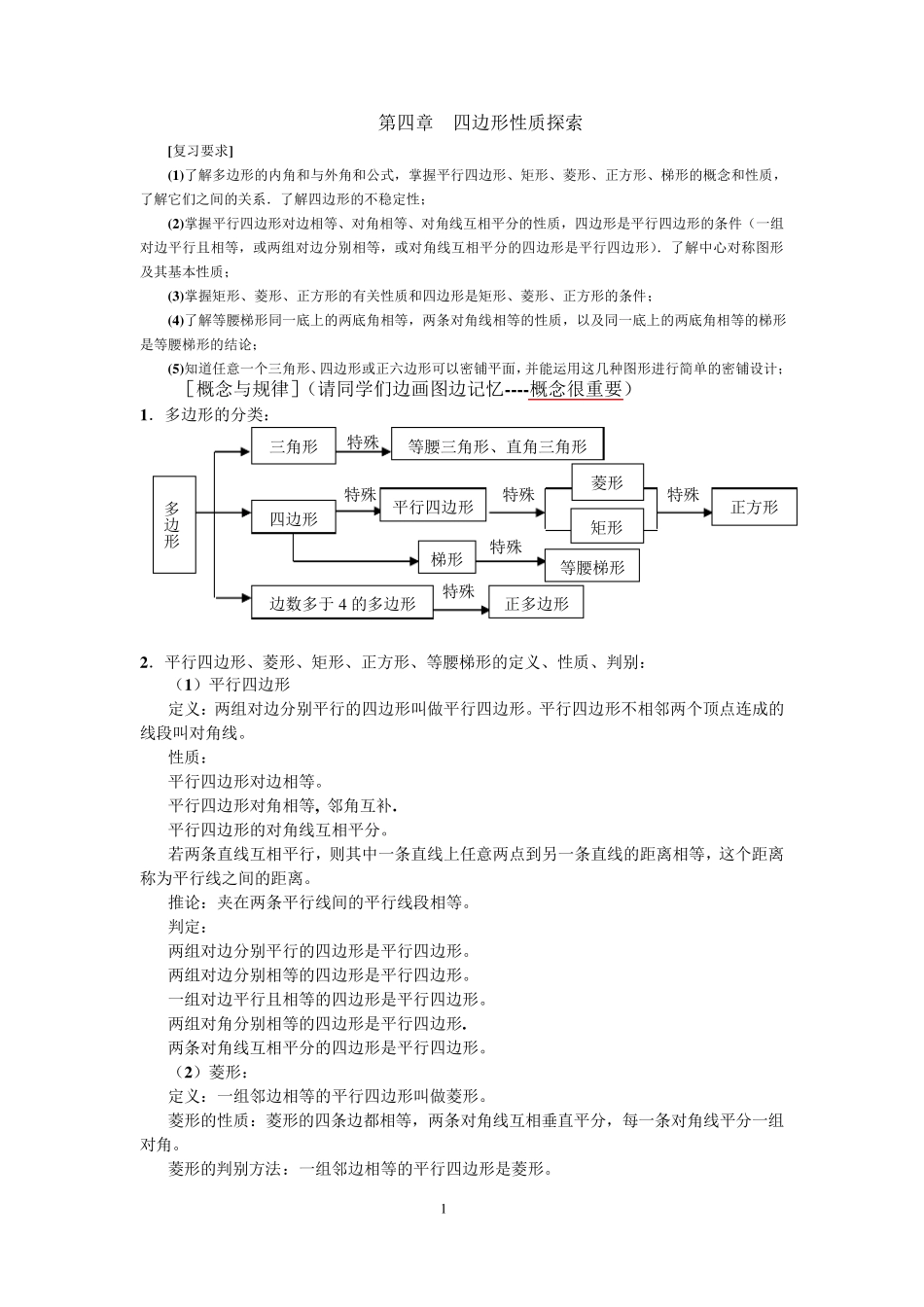
1 第四章 四边形性质探索 [复习要求] (1)了解多边形的内角和与外角和公式,掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系.了解四边形的不稳定性; (2)掌握平行四边形对边相等、对角相等、对角线互相平分的性质,四边形是平行四边形的条件(一组对边平行且相等,或两组对边分别相等,或对角线互相平分的四边形是平行四边形).了解中心对称图形及其基本性质; (3)掌握矩形、菱形、正方形的有关性质和四边形是矩形、菱形、正方形的条件; (4)了解等腰梯形同一底上的两底角相等,两条对角线相等的性质,以及同一底上的两底角相等的梯形是等腰梯形的结论; (5)知道任意一个三角形、四边形或正六边形可以密铺平面,并能运用这几种图形进行简单的密铺设计; [概念与规律](请同学们边画图边记忆----概念很重要) 1.多边形的分类: 2.平行四边形、菱形、矩形、正方形、等腰梯形的定义、性质、判别: (1)平行四边形 定义:两组对边分别平行的四边形叫做平行四边形。平行四边形不相邻两个顶点连成的线段叫对角线。 性质: 平行四边形对边相等。 平行四边形对角相等, 邻角互补. 平行四边形的对角线互相平分。 若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离。 推论:夹在两条平行线间的平行线段相等。 判定: 两组对边分别平行的四边形是平行四边形。 两组对边分别相等的四边形是平行四边形。 一组对边平行且相等的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形. 两条对角线互相平分的四边形是平行四边形。 (2)菱形: 定义:一组邻边相等的平行四边形叫做菱形。 菱形的性质:菱形的四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角。 菱形的判别方法:一组邻边相等的平行四边形是菱形。 特殊 菱形 矩形 特殊 正方形 多边形 三角形 等腰三角形、直角三角形 四边形 特殊 梯形 特殊 等腰梯形 边数多于 4 的多边形 特殊 正多边形 平行四边形 特殊 2 对角线互相垂直的平行四边形是菱形. 对角线互相垂直平分的四边形是菱形。 四条边都相等的四边形是菱形。 菱形的面积等于两条对角线乘积的一半(面积计算,即S 菱形=L1.L2/2)。 (3)矩形: 定义:有一个内角是直角的平行四边形叫做矩形。 矩形的性质:矩形的对角线相等;四个角都是直角。 矩形的判别方法:有一个角是直...