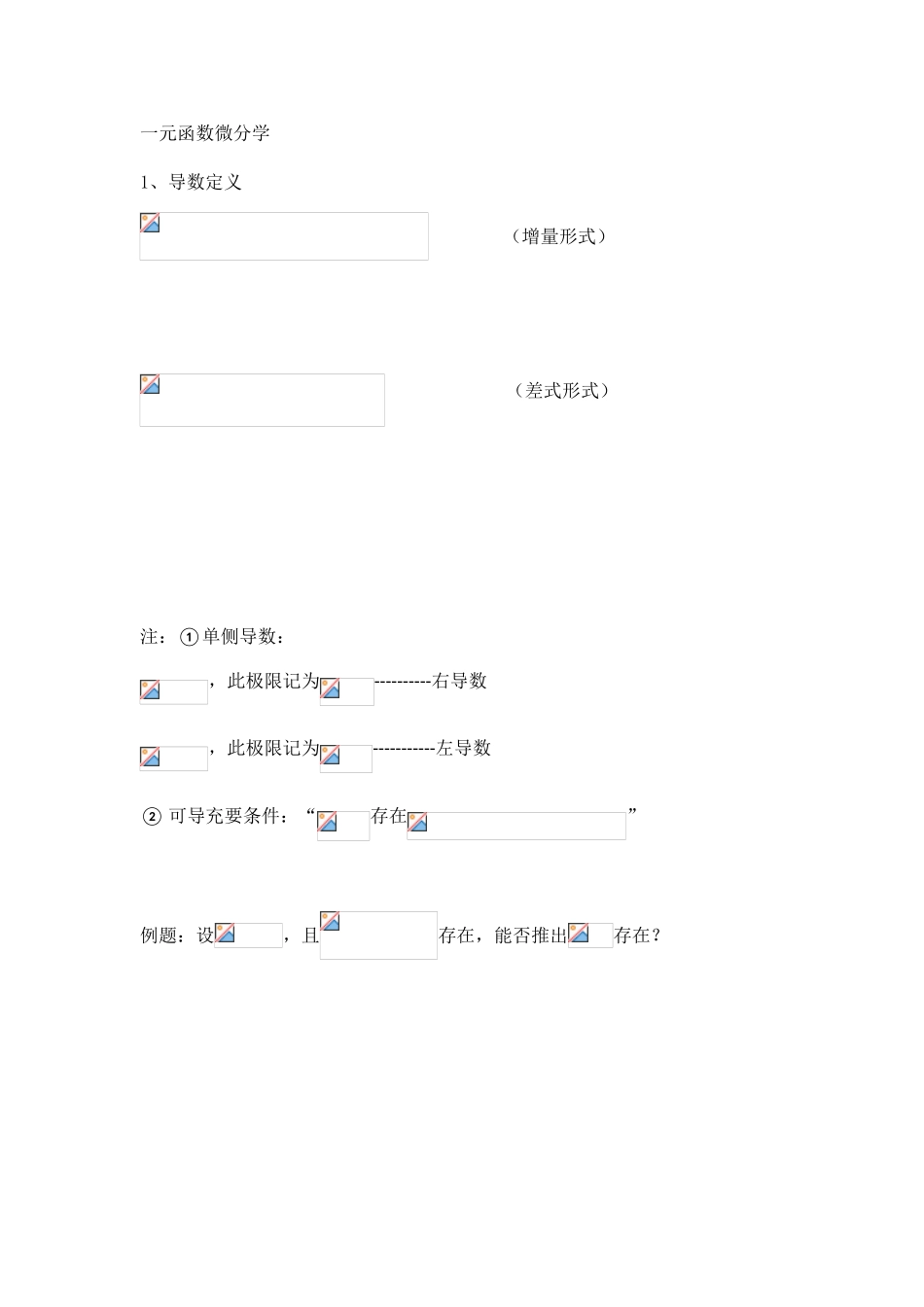
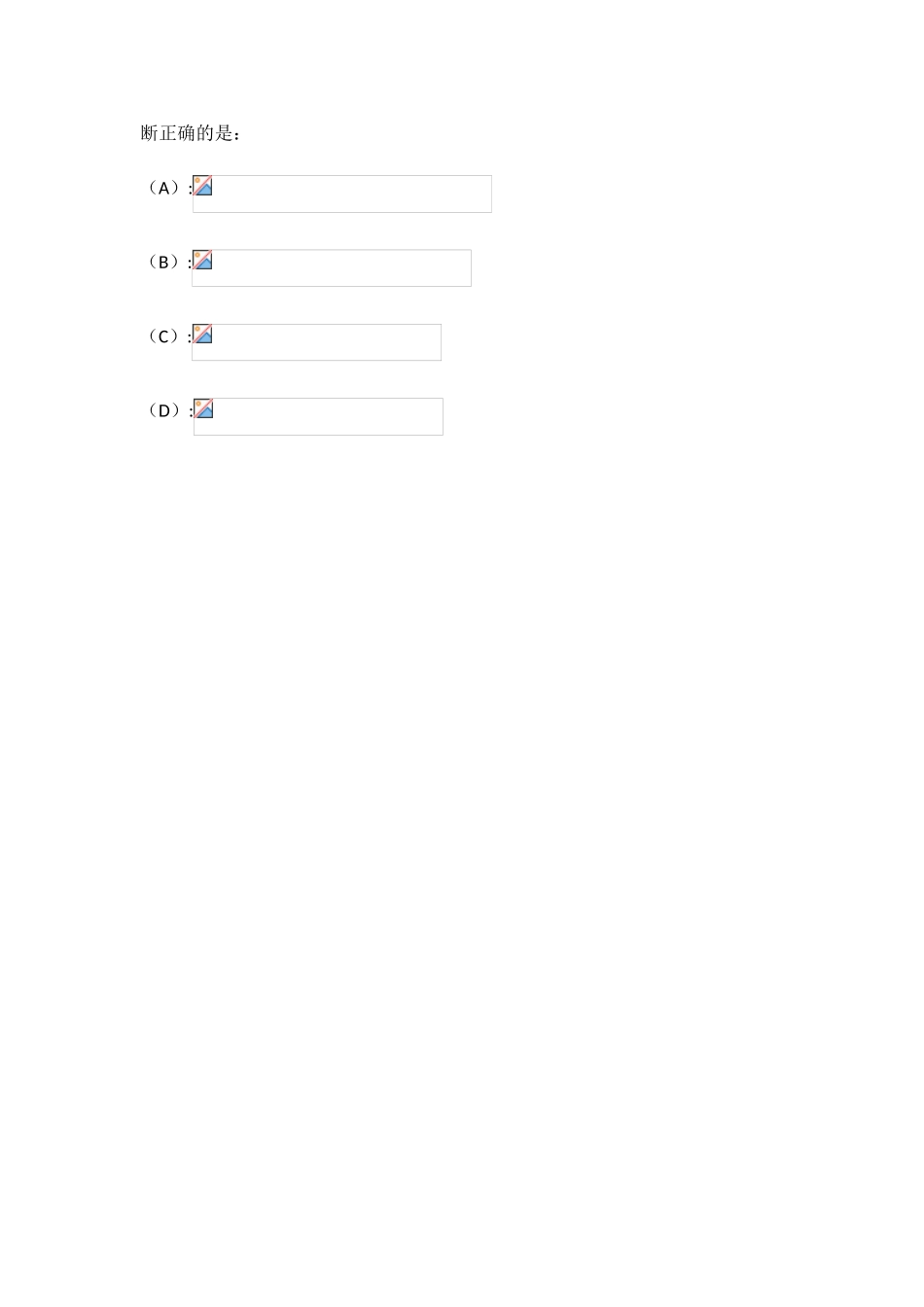
一元函数微分学1、导数定义(增量形式)(差式形式)注:①单侧导数:,此极限记为----------右导数,此极限记为-----------左导数②可导充要条件:“存在”例题:设,且存在,能否推出存在?答案:不能例题:设,则在可导的充分条件是()A存在B存在C存在D存在答案:B若C选项换为,怎样?例题:设在的某个邻域内有定义,则在处可导的一个充分条件是()A存在B存在C存在D存在例题:设的某去心邻域内可导。下述论断正确的是:(A):(B):(C):(D):中值定理:微分及计算①定义-----函数在点邻域内有定义,当自变量在点处有增量时,若相应的函数增量可以表示为,其中是不依赖的常数,是时比高阶的无穷小量,则称在点处是可微的,其中的线性主部称为在点相应于自变量增量的微分,记作.易证,故与微分相关的常用公式;一阶微分形式不变性:设,则,即不论是自变量还是中间变量,形式是不变的②微分的几何意义如图所示,是曲线在点相应于自变量增量的纵坐标增量,微分是曲线在点处的切线纵坐标相应的增量.例题:设具有二阶导数,且,为自变量在点处的增量,与分别为在点处对应的增量与微分,若,则()ABCD答案:A③微分计算如果函数在点处可导且满足,则函数在点处的微分为,可以把微分计算转化为求导的运算.例题:若函数有,则当时,函数在处的微分是()A与等价的无穷小B与同价的无穷小C比低价的无穷小D比高价的无穷小答案:B例:设函数可导,,当自变量在处取得增量时,相应的函数增量的线性主部为0.1,则()A-1B0.1C1D0.5答案:D