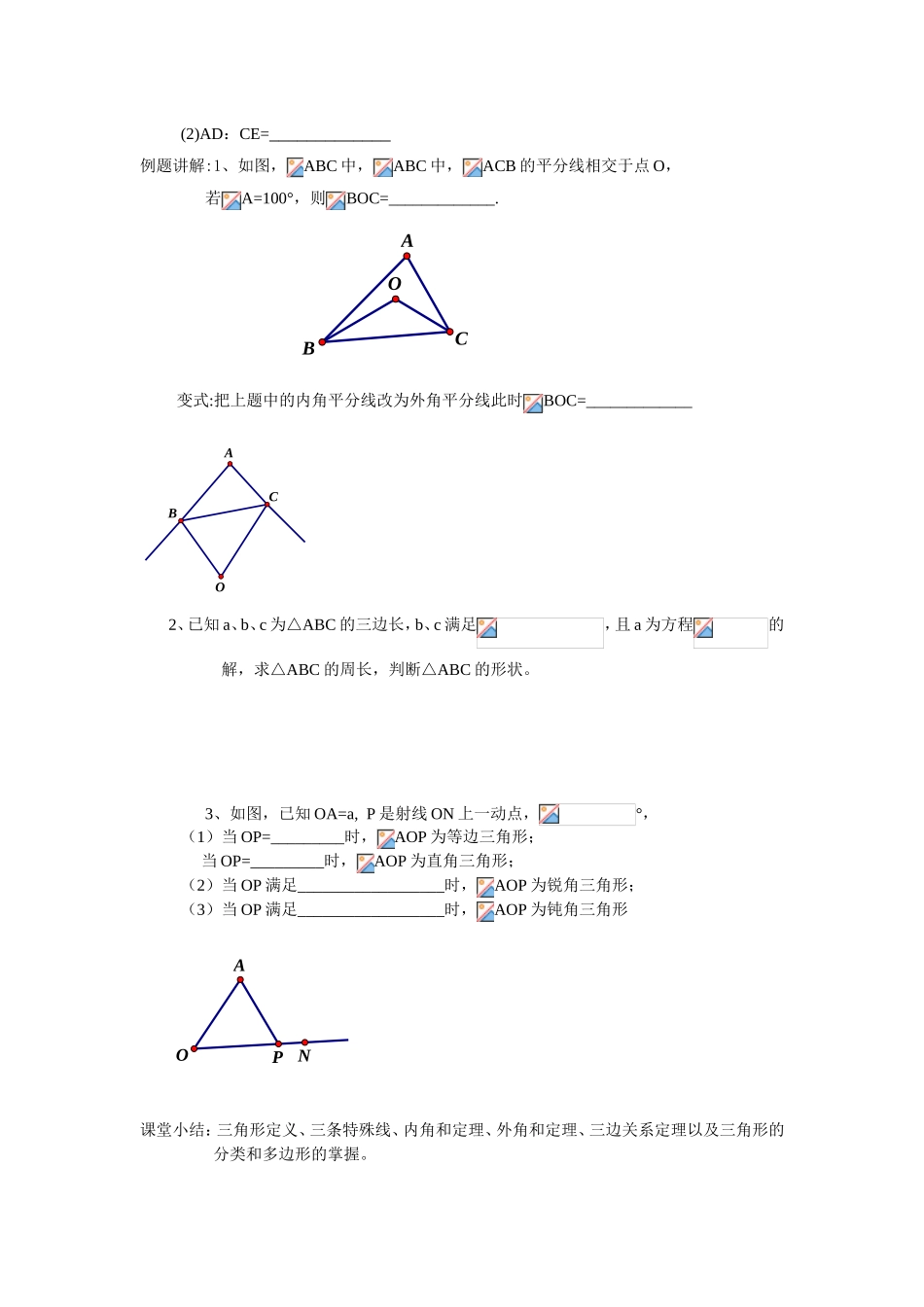
复习三角形的概念复习目标:了解三角形的有关概念和三角形的分类,会画三角形的三条线,多边形(正多边形)的定义及有关概念;了解三角形的稳定性;掌握三角形内角和外角和定理;能够运用方程的方法解决几何题。重点:三角形的有关概念难点:三角形中定理和概念的运用预习作业:1、三角形概念和分类(1)三角形定义:由_____________.所组成的图形叫做三角形。(2)三角形的分类:按边分为_____________,按角分为_____________2、三角形的性质(1)三角形三边的关系:_____________,_____________。(2)三角形的内角和定理:__________________________。(3)三角形的外角及性质:__________________________。(4)三角形的特性:_____________________3、多边形(正多边形)的定义及其有关概念(内角,外角,对角线)(1)n多边形的内角和等于_________;多边形的外角和等于__________;n多边形的对角线条数为_________。(2)镶嵌:用一些不_______摆放的多边形把平面的一部分_______;叫做用多边形覆盖平面(或平面镶嵌)。方法规律:平面镶嵌的条件是在某一点拼在一起的几个多边形的内角和为360°3、一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是()A.14B.15C.16D.174、用m个正三角形和n个正六边形地砖铺满地面,m、n的值为_____________.5、如图,ABC中,AB=2,BC=4,(1)作ABC的高AD与CE;(2)AD:CE=_____________例题讲解:1、如图,ABC中,ABC中,ACB的平分线相交于点O,若A=100°,则BOC=_____________.ABCO变式:把上题中的内角平分线改为外角平分线此时BOC=_____________ABCO2、已知a、b、c为△ABC的三边长,b、c满足,且a为方程的解,求△ABC的周长,判断△ABC的形状。3、如图,已知OA=a,P是射线ON上一动点,°,(1)当OP=_________时,AOP为等边三角形;当OP=_________时,AOP为直角三角形;(2)当OP满足__________________时,AOP为锐角三角形;(3)当OP满足__________________时,AOP为钝角三角形AOPN课堂小结:三角形定义、三条特殊线、内角和定理、外角和定理、三边关系定理以及三角形的分类和多边形的掌握。课堂检测:来源:学科网]1、如果三角形的两边分别为3和5,那么连接这个三角形三边中点,所得的三角形的周长可能是()A.4B.4.5C.5D.5.52、已知的一个外角为50°则一定是()A.锐角三角形B.钝角三角形[来源:Zxxk.Com]C.直角三角形D.钝角三角形或锐角三角形[来源:学科网]3、如图,,100°,则()A20°B25°C30°D40°4、一个凸边形的内角和是540°,那么这个多边形的对角线条数是()A5B4C3D25、,AD是高,AE、BF是角平分线相交于点O,°,°,。oABCDFE6、一个零件的形状如图,按规定应等于90度,32°和21°,检验工人量得,就判断这个零件不合格。运用三角形知识说明零件不合格的理由。CABD课后作业1、已知△ABC的周长为18cm,a、b、c为三边,且a+b=2c,a:b=1:2,则a=。2、(2006年黑龙江省)一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是()A.14B.15C.16D.173、(2006年辽宁)已知点I为△ABC的内心,∠BIC=130°,则∠BAC的度数是()A.65°B.75°C.80°D.100°4、如图所示,将长方形ABCD沿AE折叠,使点D落在BC上的点F处。若∠BAF=600,则∠DAE=度。5、。MHGABEFCD(选做)1、在中,AB=AC,AC上的中线BD把的周长分为12cm和18cm,求三角形的各边长。2、已知等腰三角形的周长为23cm,其中两边之差为5cm,求腰和底边的长