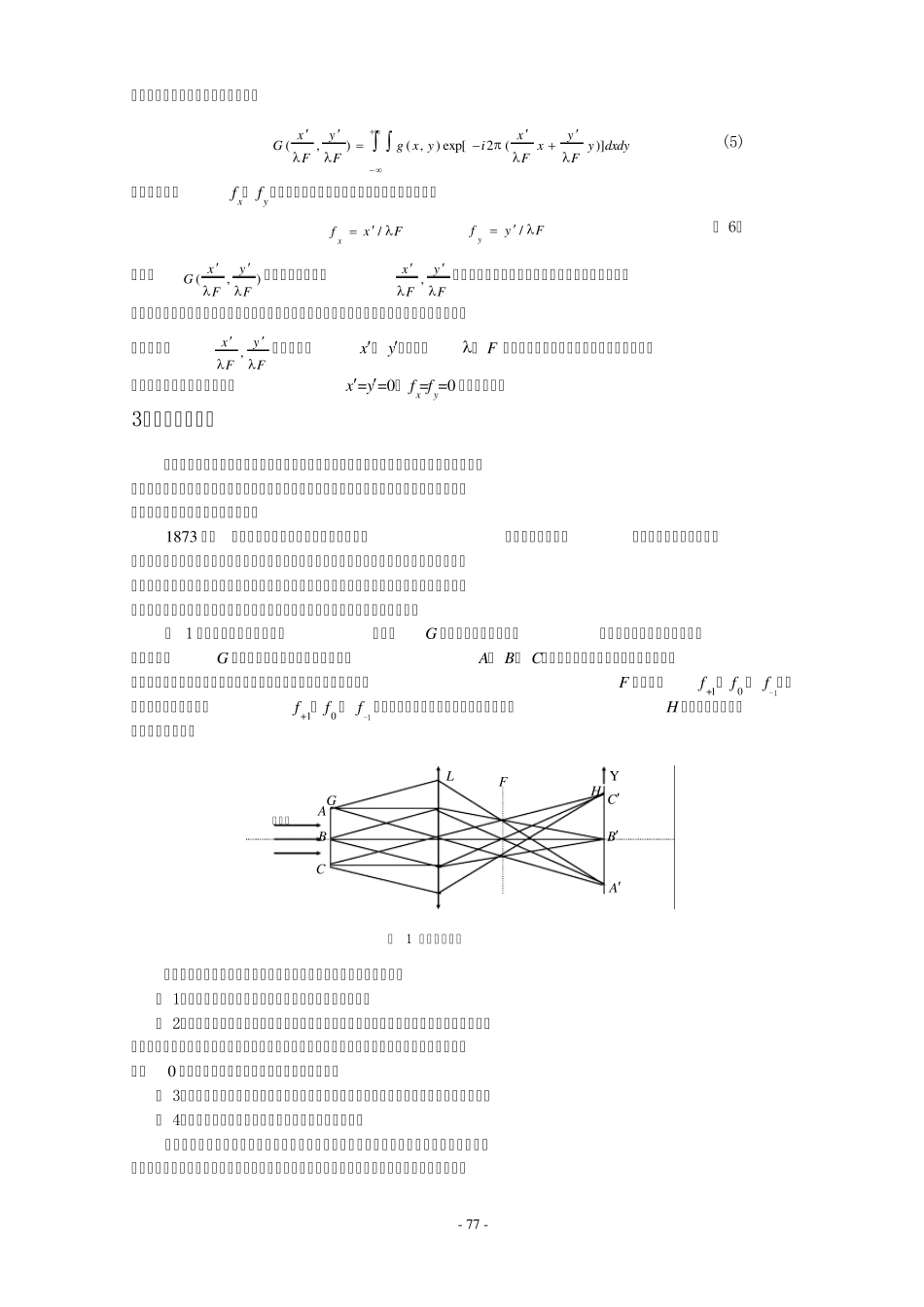
- 7 5 - 傅立叶光学的空间频谱与 空间滤波实验 实 验 说 明 书 北 京 方 式 科 技 有 限 责 任 公 司 - 76 - 实验目的 1、了解透镜的傅里叶变换性质,加深对空间频率、空间频谱和空间滤波等概念的理解。 2、熟悉阿贝成像原理,从信息量的角度理解透镜孔径对分辨率的影响。 3、完成一维空间滤波、二维空间滤波及高通空间滤波。 实验原理 1873年阿贝(E.Abbe)首先提出显微镜成像原理以及随后的阿贝—波特空间滤波实验,在傅里叶光学早期发展史上做出重要的贡献。这些实验简单、形象,令人信服,对相干光成像的机理及频谱分析和综合原理做出深刻的解释,同时这种用简单的模板作滤波的方法一直延续至今,在图像处理技术中仍然有广泛的应用价值。 1、二维傅里叶变换和空间频谱 在信息光学中常用傅里叶变换来表达和处理光的成像过程。设在物屏X-Y平面上光场的复振幅分布为g (x, y) ,根据傅里叶变换特性,可以将这样一个空间分布展开成一系列二维基元函数)](2ex p[yfxfiyx的线性叠加,即 yxyxyxdfdfyfxfiffGyxg)](2ex p[),(),( ( 1) 式中fx、 fy为 x、 y方向的空间频率,即单位长度内振幅起伏的次数,G (fx, fy)表示原函数g (x, y)中相应于空间频率为fx、 fy 的基元函数的权重,亦即各种空间频率的成分占多大的比例,也称为光场(optical field) g (x, y)的空间频谱。G (fx、 fy)可由g (x, y)的傅里叶变换求得 dxdyyfxfiyxgffGyxyx)](2ex p[),(),( (2) g(x, y)与 G (fx, fy)是一对傅里叶变换式,G (fx, fy)称为g(x, y)的傅里叶的变换,g(x, y)是 G (fx, fy)的逆变换,它们分别描述了光场的空间分布及光场的频率分布,这两种描述是等效的。 当 g(x, y)是空间周期函数时,空间频率是不连续的。例如空间周期为x0 的一维函数g(x),即g(x)=g (x+x0)。描述空间周期为x0 的一维光栅时,光栅面上光振幅分布可展成傅里叶级数 )2ex p()2ex p()(0 xnfiGxfiGxgnnn (3) 上式中,n= 0,±1,±2,„„;f0=1/x0 ,称为基频;fn=nf0,是基频的整数倍频,称为n 次谐波的频率。Gn 是 g(x)的空间频率,由傅里叶变换得 dxxnfixgxGxxn)2ex p()(102/2/000 (4) 2、透镜的二维傅里叶变换性质 在光学上,透镜是一个傅里叶变换器,它具有二维傅里叶变换的本领。理论证明,若在焦距为 ...