实验二时域采样与频域采样及MATLAB程序

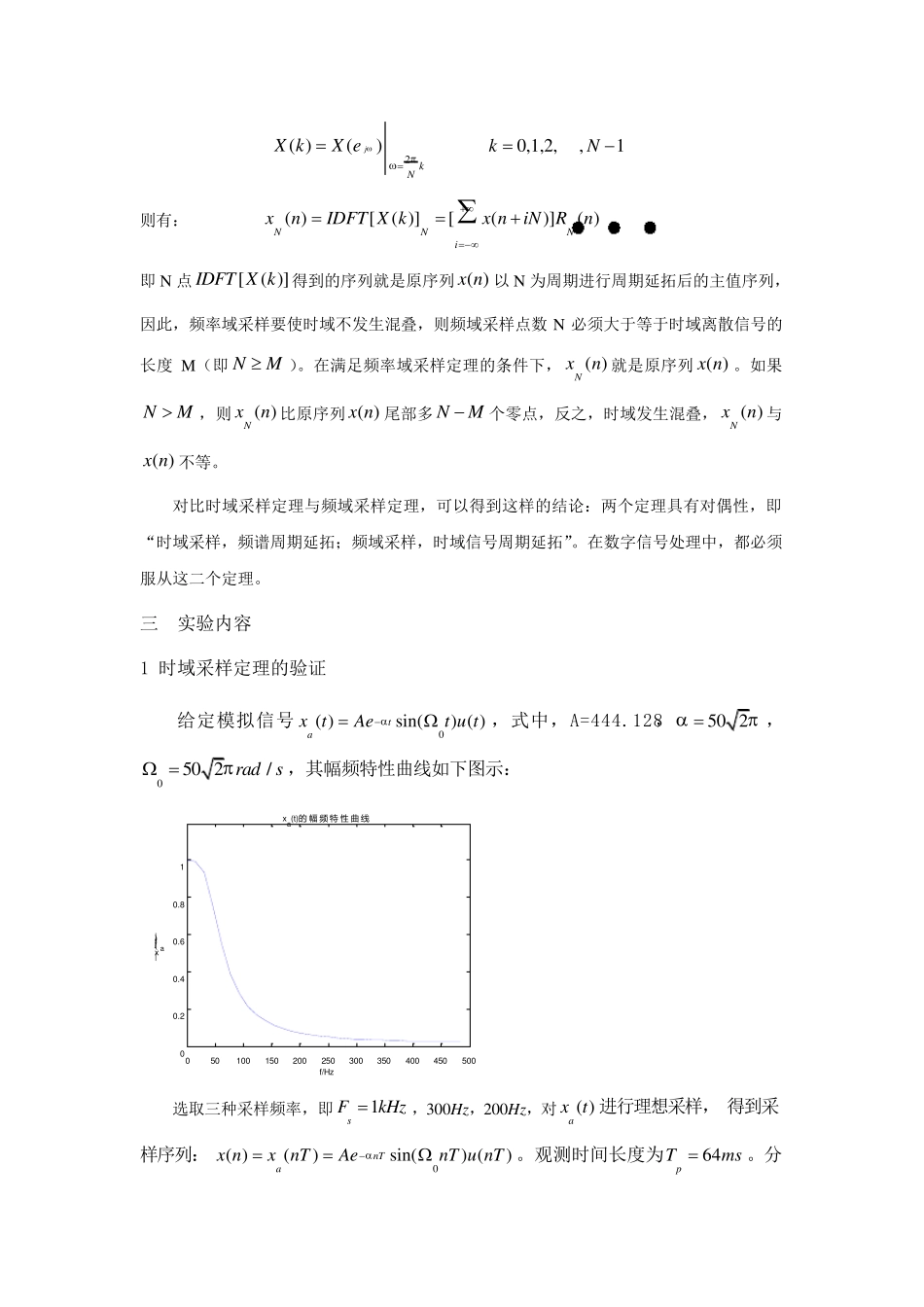
实验二 时域采样与频域采样 一 实验目的 1 掌握时域连续信号经理想采样前后的频谱变化，加深对时域采样定理的理解 2 理解频率域采样定理，掌握频率域采样点数的选取原则 二 实验原理 1 时域采样定理 对模拟信号( )axt 以T 进行时域等间隔采样，形成的采样信号的频谱ˆ ()aXj会以采样角频率2()ssT  为周期进行周期延拓，公式为： 1ˆˆ()[ ( )]()aaasnXjFT xtXjjnT   利用计算机计算上式并不容易，下面导出另外一个公式。 理想采样信号ˆ ( )axt 和模拟信号( )axt 之间的关系为： ˆ ( )( )()aanxtxttnT 对上式进行傅里叶变换，得到： ˆ ()[ ( )()( ) ()j tj taaannXjxttnT edtxttnT edt    在上式的积分号内只有当tnT时，才有非零值，因此 : ˆ ()()jnTaanXjxnT e   上式中，在数值上()( )axnTx n，再将T  代入，得到： ˆ ()( )()jnjaaTTnXjxn eX e  上式说明采样信号的傅里叶变换可用相应序列的傅里叶变换得到，只要将自变量 用T代替即可。 2 频域采样定理 对信号( )x n 的频谱函数()jX e 在[0，2 ]上等间隔采样N 点，得到 2( )()jkNX kX e  0,1,2,,1kN 则有： ( )[( )][()]( )NNNixnIDFT X kx niNRn 即N 点[( )]IDFT X k得到的序列就是原序列( )x n 以N 为周期进行周期延拓后的主值序列， 因此，频率域采样要使时域不发生混叠，则频域采样点数N 必须大于等于时域离散信号的长度M（即NM）。在满足频率域采样定理的条件下，( )Nxn 就是原序列( )x n 。如果NM，则( )Nxn 比原序列( )x n 尾部多NM个零点，反之，时域发生混叠，( )Nxn 与( )x n 不等。 对比时域采样定理与频域采样定理，可以得到这样的结论：两个定理具有对偶性，即“时域采样，频谱周期延拓；频域采样，时域信号周期延拓”。在数字信号处理中，都必须服从这二个定理。 三 实验内容 1 时域采样定理的验证 给定模拟信号0( )sin() ( )tax tAet u t，式中，A=444.128，50 2，050 2/rad s ，其幅频特性曲线如下图示： 05010015020025030035040045050000.20.40.60.81f/Hz|x...