实验五1实验五信号的抽样与恢复

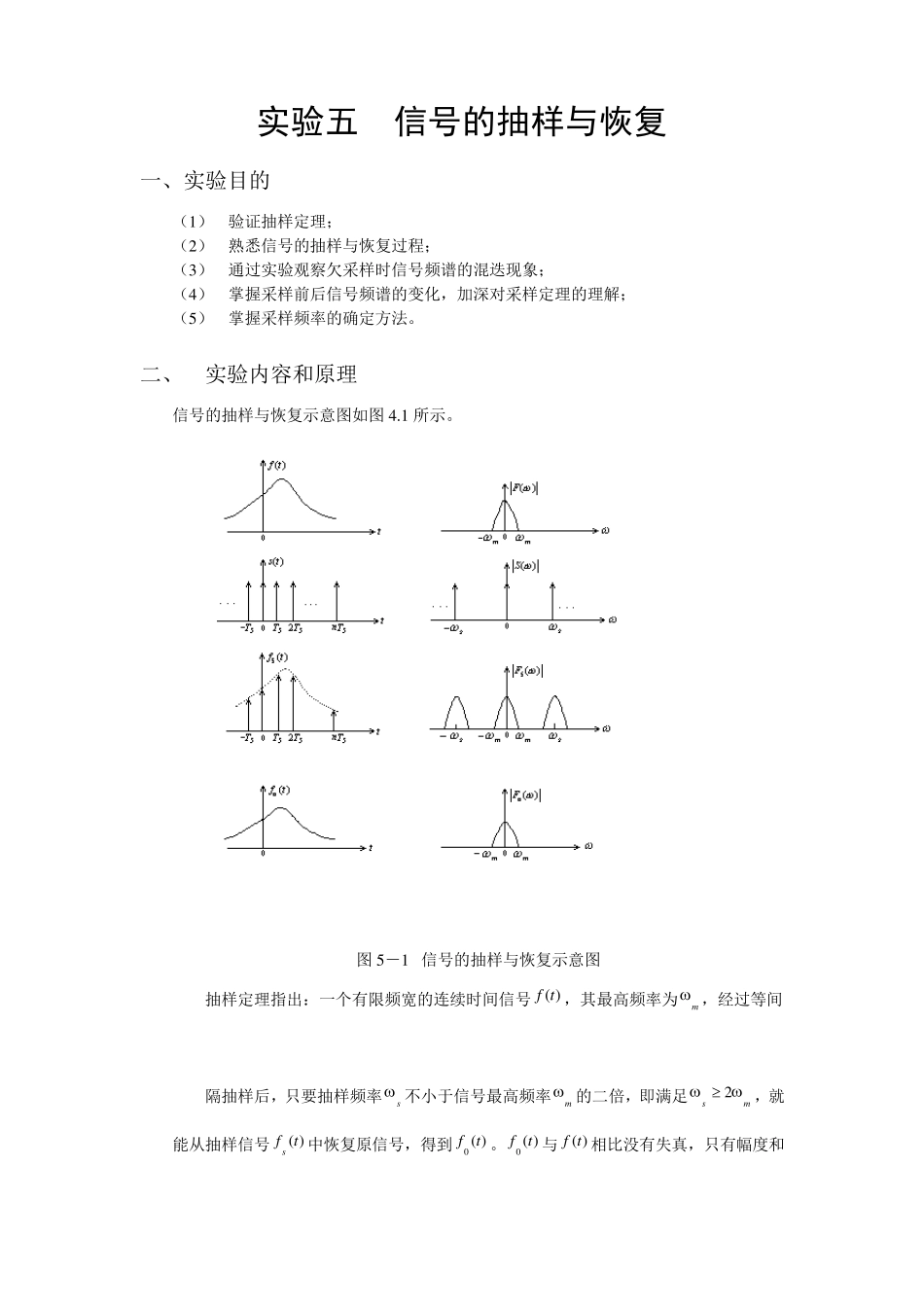
实验五 信号的抽样与恢复 一、实验目的 （1 ） 验证抽样定理； （2 ） 熟悉信号的抽样与恢复过程； （3 ） 通过实验观察欠采样时信号频谱的混迭现象； （4 ） 掌握采样前后信号频谱的变化，加深对采样定理的理解； （5 ） 掌握采样频率的确定方法。 二、 实验内容和原理 信号的抽样与恢复示意图如图 4 .1 所示。 图 5 －1 信号的抽样与恢复示意图 抽样定理指出：一个有限频宽的连续时间信号)(tf，其最高频率为m ，经过等间 隔抽样后，只要抽样频率s 不小于信号最高频率m 的二倍，即满足ms2，就能从抽样信号)(tfs中恢复原信号，得到)(0 tf。)(0 tf与)(tf相比没有失真，只有幅度和相位的差异。一般把最低的抽样频率ms2min 称为奈奎斯特抽样频率。当 ms2时，)(tfs的频谱将产生混迭现象，此时将无法恢复原信号。 )(tf的幅度频谱为 )(F；开关信号)(ts为周期矩形脉冲，其脉宽 相对于周期sT 非常小，故将其视为冲激序列，所以)(ts的幅度频谱)(S亦为冲激序列；抽样信号)(tfs的幅度频谱为)(sF；)(0 tf的幅度频谱为)(0 F。如图4.1 所示。 观察抽样信号的频谱)(sF，可以发现利用低通滤波器（其截止频率满足mscm）就能恢复原信号。 信号抽样与恢复的原理框图如图4.2 所示。 图 5－2 信号抽样与恢复的原理框图 由原理框图不难看出，A/D 转换环节实现抽样、量化、编码过程；数字信号处理环节对得到的数字信号进行必要的处理；D/A 转换环节实现数/模转换，得到连续时间信号；低通滤波器的作用是滤除截止频率以外的信号，恢复出与原信号相比无失真的信号)(0 tf。 三、涉及的MATLAB函数 subplot(2,1,1) xlabel('时间, msec');ylabel('幅值'); title('连续时间信号 x_{a}(t)'); axis([0 1 -1.2 1.2]) stem(k,xs);grid; linspace(-0.5,1.5,500)'; ones(size(n) freqs(2,[1 2 1],wa); plot(wa/(2*pi),abs(ha) buttord(Wp, Ws, 0.5, 30,'s'); [Yz, w] = freqz(y, 1, 512); M= input('欠采样因子 = '); length(nn1) y = interp(x,L) [b,a] = butter(N, Wn, 's'); get(gfp,'units'); set(gfp,'position',[100 100 400 300]); fx1=fft(xs1) abs(fx2(n2+1)) y = resample(x,L,M); 四、实验内容与方法 1. 验证性实验 1) 正弦信号的采样 MATLAB 程序: clf; t = 0:0.0005:1; f = 13; xa = cos(2*...