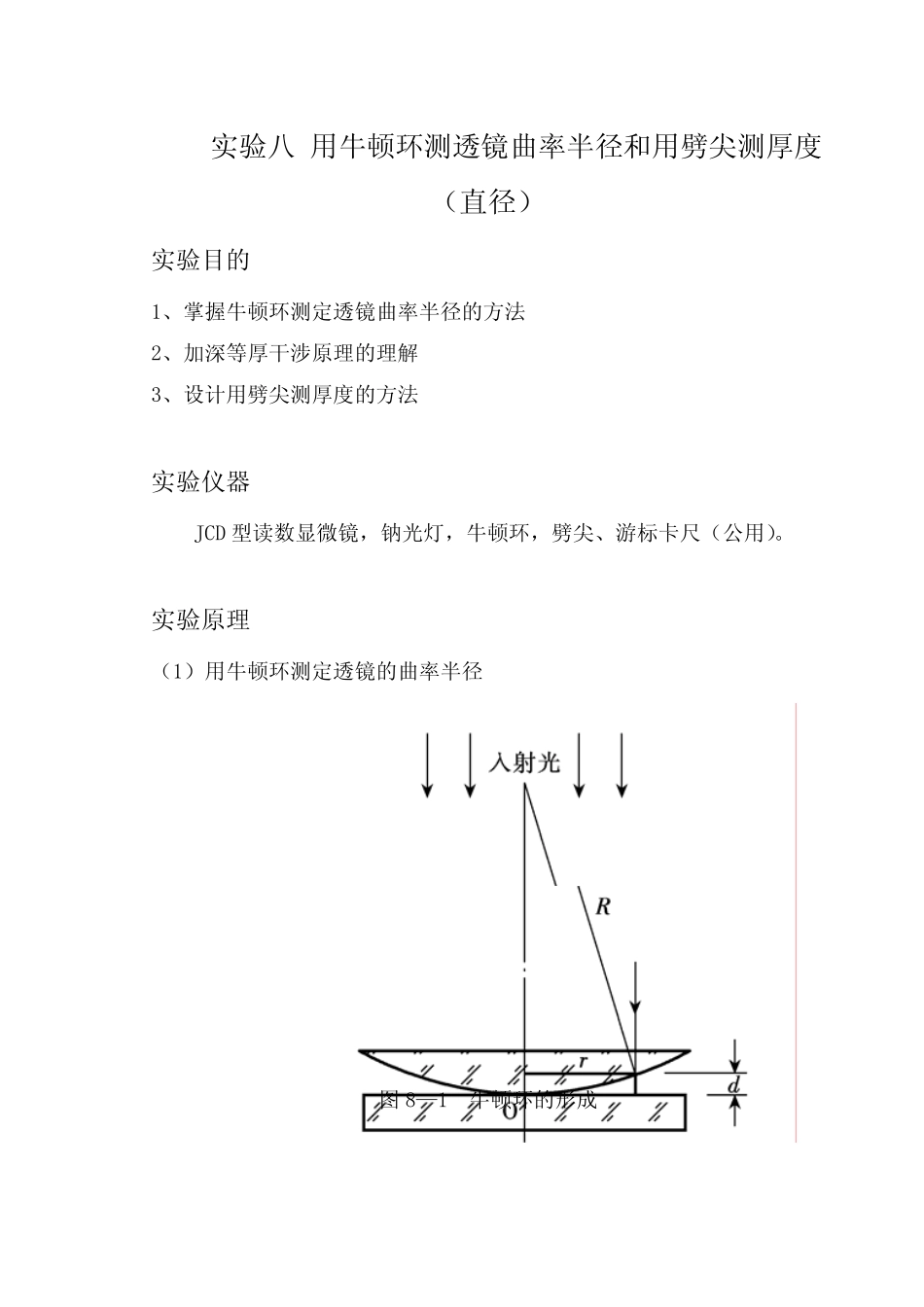
实验八 用牛顿环测透镜曲率半径和用劈尖测厚度(直径) 实验目的 1、掌握牛顿环测定透镜曲率半径的方法 2、加深等厚干涉原理的理解 3、设计用劈尖测厚度的方法 实验仪器 JCD 型读数显微镜,钠光灯,牛顿环,劈尖、游标卡尺(公用)。 实验原理 (1)用牛顿环测定透镜的曲率半径 图8—1 牛顿环的形成 图8-2 牛顿环实验装置 一个曲率半径很大的平凸透镜,以其凸面朝下,放在一块平面玻璃板上(图8—1),二者之间形成从中心向周边逐渐增厚的空气膜。若对透镜垂直投射单色平行光,则空气膜下缘面与上缘面反射的光就会在空气膜上缘面附近相遇而干涉,出现以玻璃接触点为中心的一系列明暗相间的圆环,即牛顿环。 设透镜曲率半径为R,与接触点O相距r处的膜厚为d,则 222)2(dRddRdr−=−= (8-1) 因 R>>d,所以可略去,得 2dRrd22= (8-2) 光线垂直入射,几何程差为,还要考虑光波在平面玻璃上反射会有半波损失,从而带来d22λ 的附加程差,所以总程差 22λδ+= d (8-3) 产生暗环的条件是 2)12(λδ+=m (8-4) 其中m为干涉级。综合以上 4 式,第m级暗环半径 Rmrmλ= (8-5) 实际上,由于两镜面接触点之间难免存在细微的尘埃,使程差产生难以确定的变化,中央暗点可变为亮点或若明若暗;再者,接触压力引起的玻璃形变会使接触点扩大成一个接触面,以致接近圆心处的干涉条纹也是宽阔而模糊的。这就给m带来某种程度的不确定性。根据式(8-5),可得 λλnRrmRrnm==22, (8-6) 两式相减得 λRnmrrnm)(22−=− (8-7) 所以 λ)(22nmrrRnm−−= (8-8) 因m和n有着相同的不确定程度,利用m-n这一相对性测量恰好消除了由绝对测量的不确定性带来的误差。故改用测量直径。则有: λ)(422nmDDRnm−−= (8-9) 这里需注意直径两端的m 和 n 值不能数错。 实验中为了减小误差,将测得的数据分组,算出22nmDD−,从而得: λ)(422nmDDRnm−−= 由上式可知,当平凸透镜的曲率半径R 为已知时,用上法可测入射光波的波长。实际上购回的牛顿环的平凸透镜的曲率半径均为已知。 (2)利用劈形膜干涉测薄片厚度 图8—3 劈形膜 在叠合的两块平板玻璃的一端夹一薄片,即构成空气的劈形膜(见图8-3)。在单色光垂直照射下,可见空气膜上形成平行于两块玻璃面交线的等距干涉条纹。据式(3),形成暗条纹的条件为 ...2,1,0 ,2)12(22=+=+=kkdλλδ (8-10) 与k级暗条纹对应的空气膜厚度 2...