实验六线性系统的根轨迹

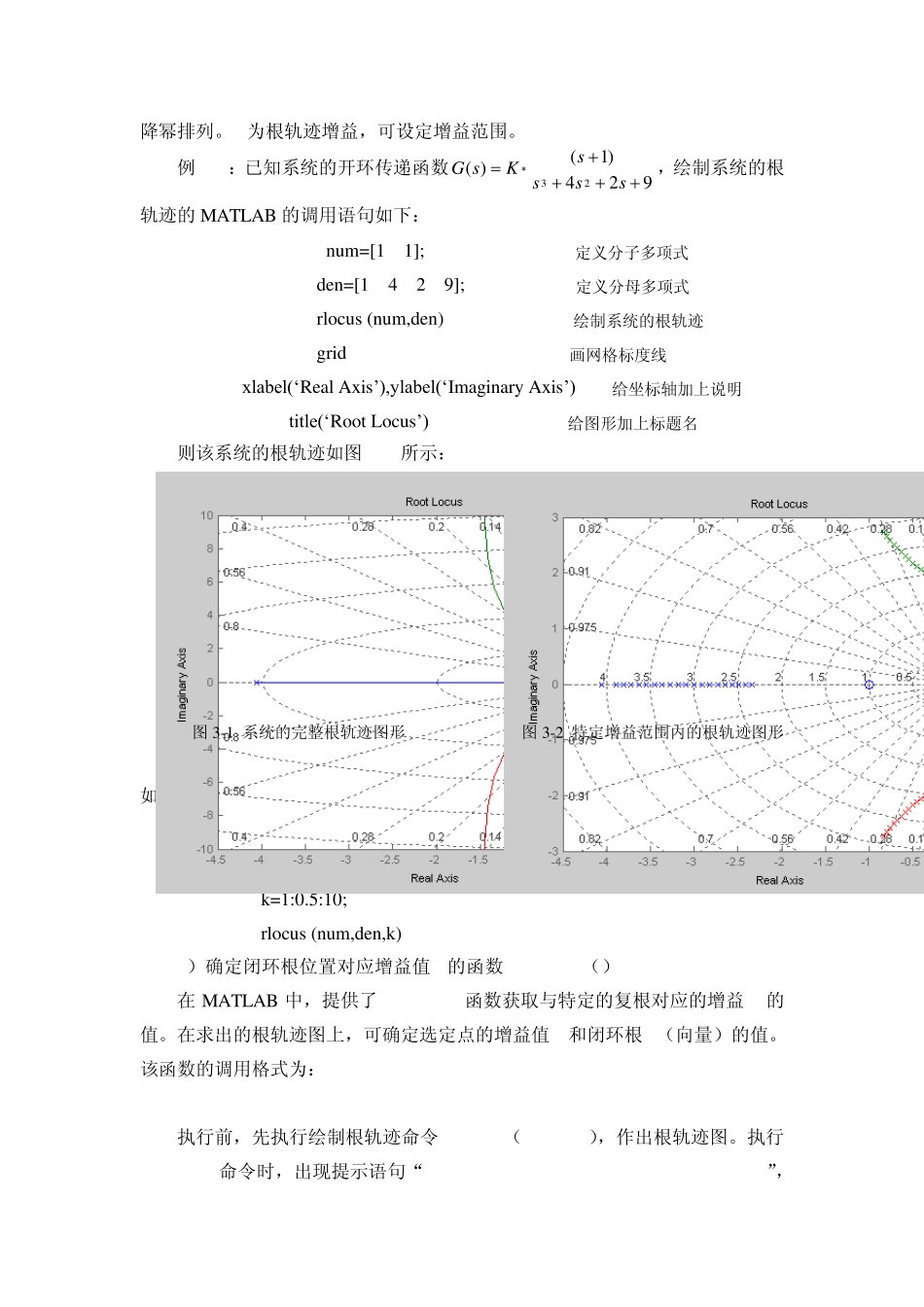
实验六 线性系统的根轨迹 一、实验目的 1. 熟悉 MATLAB 用于控制系统中的一些基本编程语句和格式。 2. 利用 MATLAB 语句绘制系统的根轨迹。 3. 掌握用根轨迹分析系统性能的图解方法。 4. 掌握系统参数变化对特征根位置的影响。 二、基础知识及 MATLAB函数 根轨迹是指系统的某一参数从零变到无穷大时，特征方程的根在 s 平面上的变化轨迹。这个参数一般选为开环系统的增益 K。课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图。而用 MATLAB 可以方便地绘制精确的根轨迹图，并可观测参数变化对特征根位置的影响。 假设系统的对象模型可以表示为 nnnnmmmmasbsasbsbsbsbKsKGsG11111210)()( 系统的闭环特征方程可以写成 0)(10sKG 对每一个 K 的取值，我们可以得到一组系统的闭环极点。如果我们改变K 的数值，则可以得到一系列这样的极点集合。 若将这些 K 的取值下得出的极点位置按照各个分支连接起来， 则可以得到一些描述系统闭环位置的曲线， 这些曲线又称为系统的根轨迹。 1）绘制系统的根轨迹 rlocus（） MATLAB 中绘制根轨迹的函数调用格式为： rlocus(num,den) 开环增益 k的范围自动设定。 rlocus(num,den,k) 开环增益 k的范围人工设定。 rlocus(p,z) 依据开环零极点绘制根轨迹。 r=rlocus(num,den) 不作图，返回闭环根矩阵。 [r,k]=rlocus(num,den) 不作图，返回闭环根矩阵r和对应的开环增益向量k。 其中，num,den分别为系统开环传递函数的分子、分母多项式系数，按 s的降幂排列。K为根轨迹增益，可设定增益范围。 例3-1：已知系统的开环传递函数924)1()(23ssssKsG，绘制系统的根轨迹的MATLAB 的调用语句如下： nu m=[1 1]; %定义分子多项式 den=[1 4 2 9]; %定义分母多项式 rlocu s (nu m,den) %绘制系统的根轨迹 grid %画网格标度线 xlabel(‘Real Ax is’),ylabel(‘Imaginary Ax is’) %给坐标轴加上说明 title(‘Root Locu s’) %给图形加上标题名 则该系统的根轨迹如图3-1所示： 若上例要绘制K在（1，10）的根轨迹图，则此时的MATLAB 的调用格式如下，对应的根轨迹如图3-2所示。 nu m=[1 1]; den=[1 4 2 9]; k=1:0.5:10; rlocu s (nu m,den,k) 2）确定闭环根位置对应增益值K的函数rlocfind（） 在MATLAB 中，提供了rlocfind函数获取与特定的复根对应的增益K的值。在求出的根...