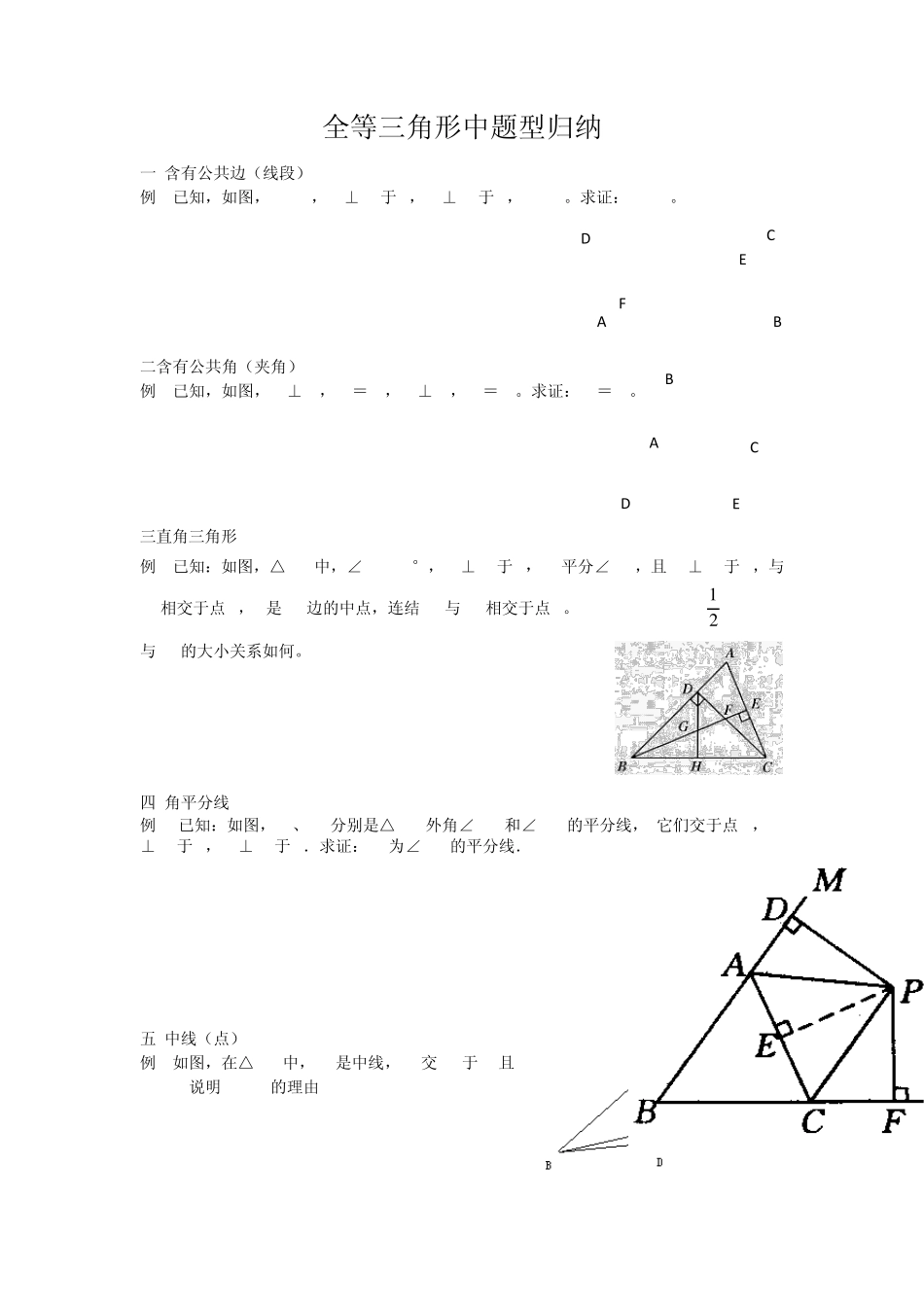
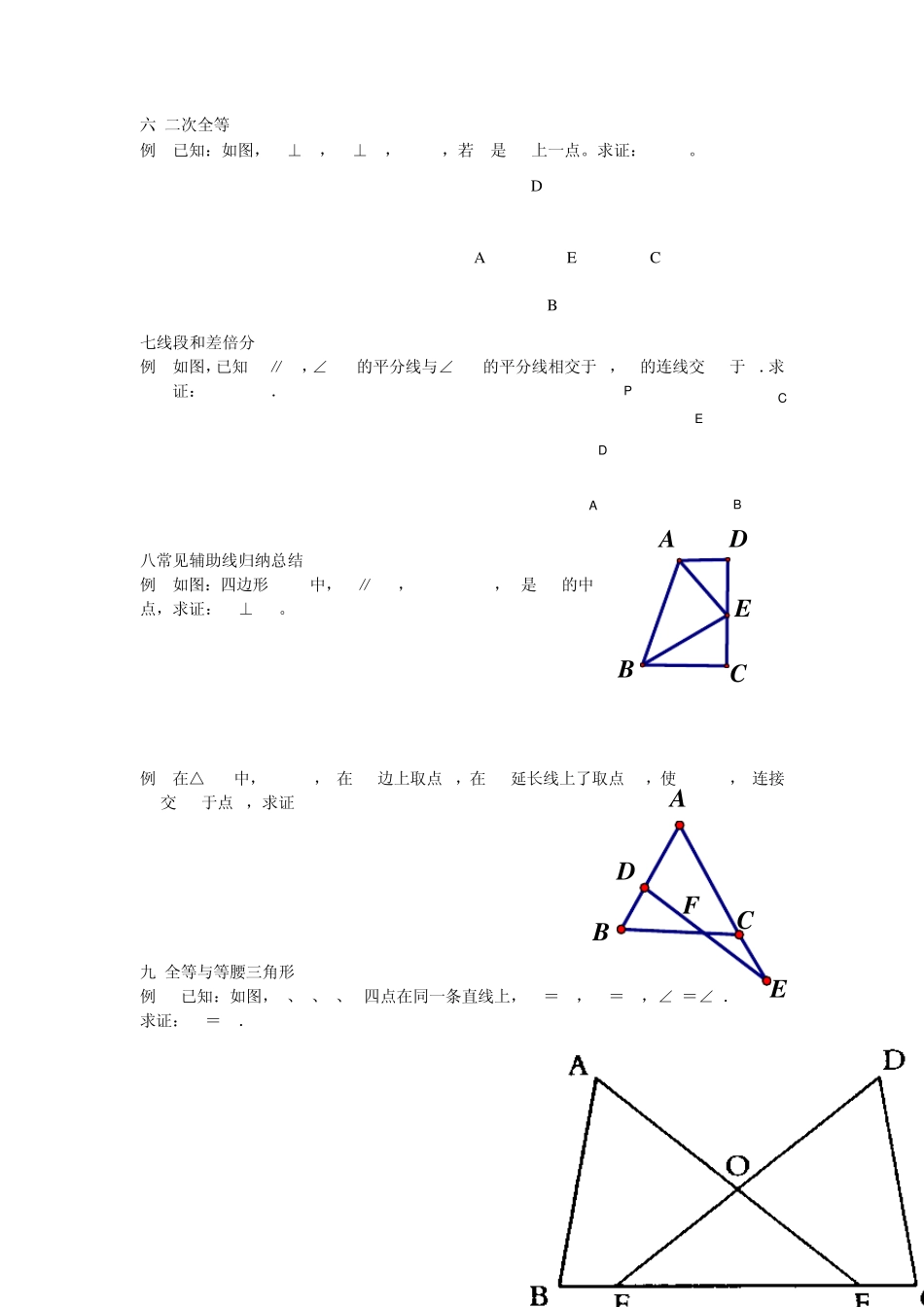
全等三角形中题型归纳 一 含有公共边(线段) 例1已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。求证:AF=CE。 二含有公共角(夹角) 例2已知,如图,AB⊥AC,AB=AC,AD⊥AE,AD=AE。求证:BE=CD。 三直角三角形 例3已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且 BE⊥AC于E,与CD相交于点 F,H是 BC边的中点,连结 DH与 BE相交于点 G。(1) BF=AC (2) CE= BF (3)CE与 BC的大小关系如何。 四 角平分线 例4.已知:如图,PA、PC分别是△ABC外角∠MAC和∠NCA的平分线,•它们交于点 P,PD⊥BM于D,PF⊥BN于F.求证:BP为∠MBN的平分线. 五 中线(点) 例5如图,在△ABC中,AD是中线,BE交 AD于F,且AE=EF,说明 AC=BF的理由 12F E A C D B A E D C B 六 二次全等 例6已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。求证:EB=ED。 D A E C B 七线段和差倍分 例7如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于 E,CE的连线交 AP于 D.求证:AD+BC=AB. 八常见辅助线归纳总结 例8如图:四边形 ABCD中,AD∥BC ,AB=AD+BC ,E是CD的中点,求证:AE⊥BE 。 例9在△ABC中,,AB=AC, 在 AB边上取点D,在 AC延长线上了取点E ,使 CE=BD , 连接DE交 BC于点F,求证DF=EF . 九 全等与等腰三角形 例10已知:如图,B、E、F、C四点在同一条直线上,AB=DC,BE=CF,∠B=∠C. 求证:OA=OD. PEDCBAADBCEFCBAEDB A O D C E 图8 十全等与等边三角形(提高) 例11(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;(2)如图8,Δ OAB固定不动,保持Δ OCD的形状和大小不变,将Δ OCD绕着点O旋转(Δ OAB和Δ OCD不能重叠),求∠AEB的大小. 十一运动与探索(提高) 20.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且 AD⊥MN于D,BE⊥MN于E. (1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE; (2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE; (3)当直线MN绕点C旋转到图3的位置时,试问 DE,AD,BE具有怎样的等量关系?请写出这个等量关系,并加以证明. C B O D 图7 A E C B A E D 图1 N M A B C D E M N 图2 A C B E D N M 图3 课后练习 1如图,在△ABC和△D...