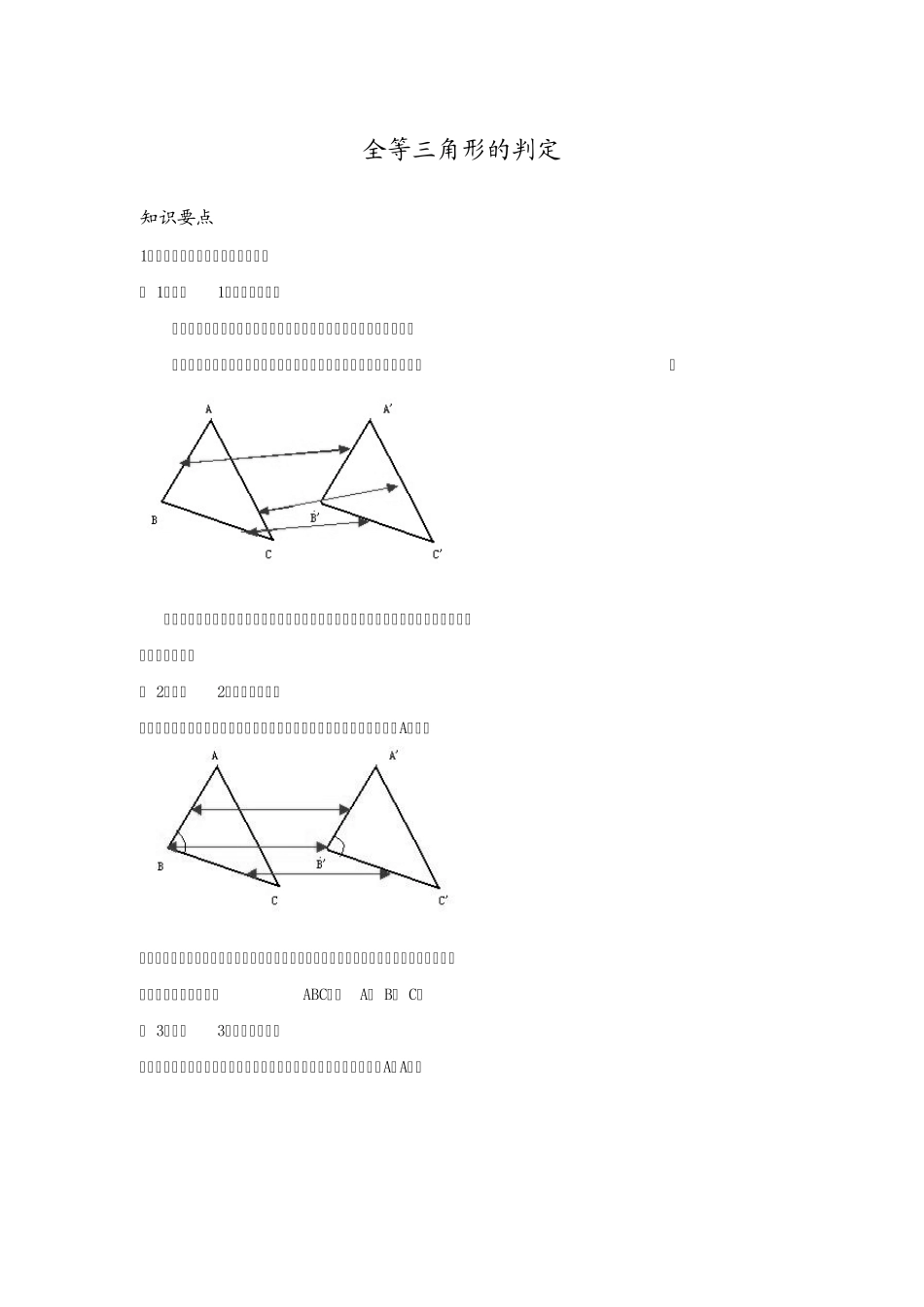
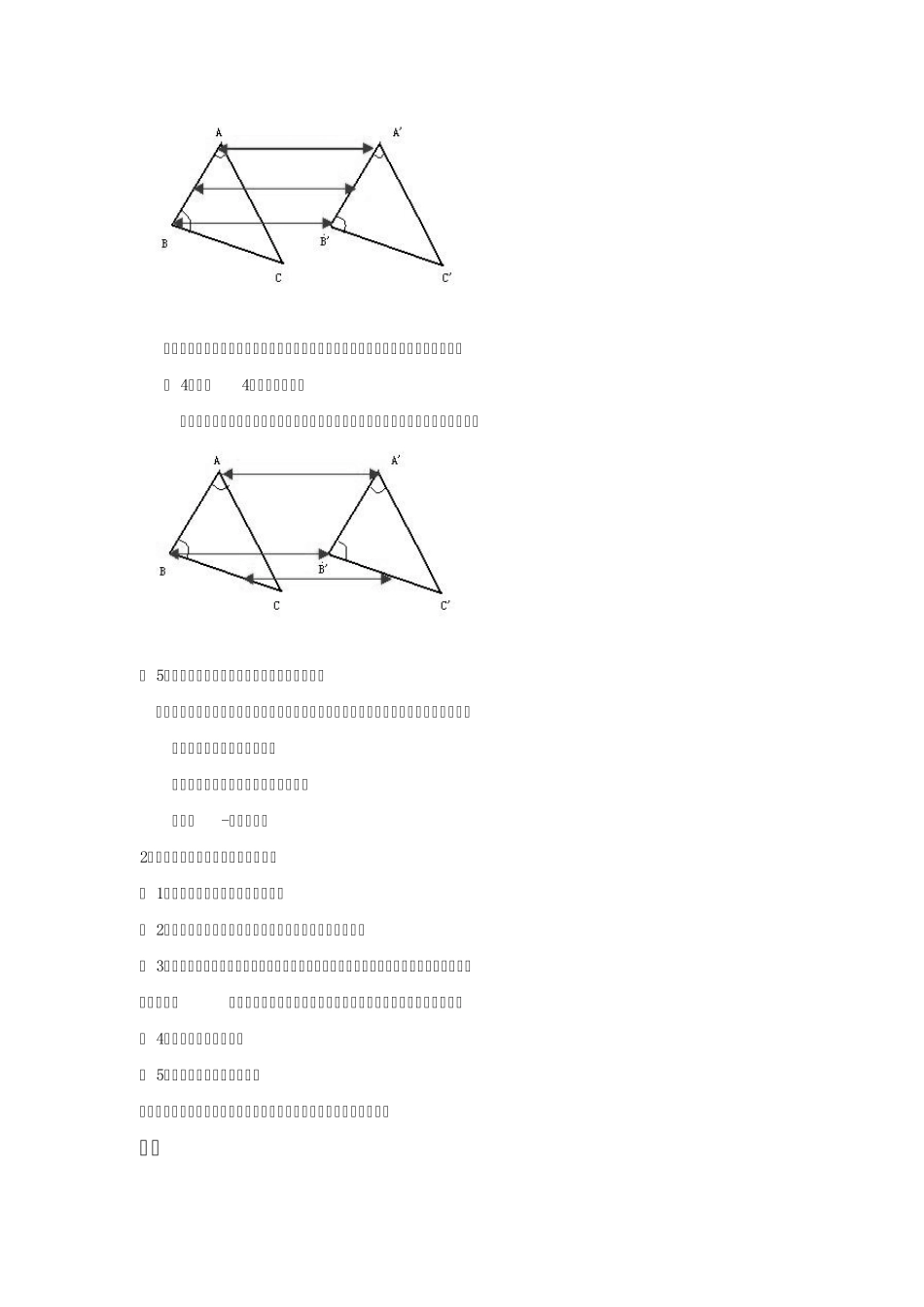
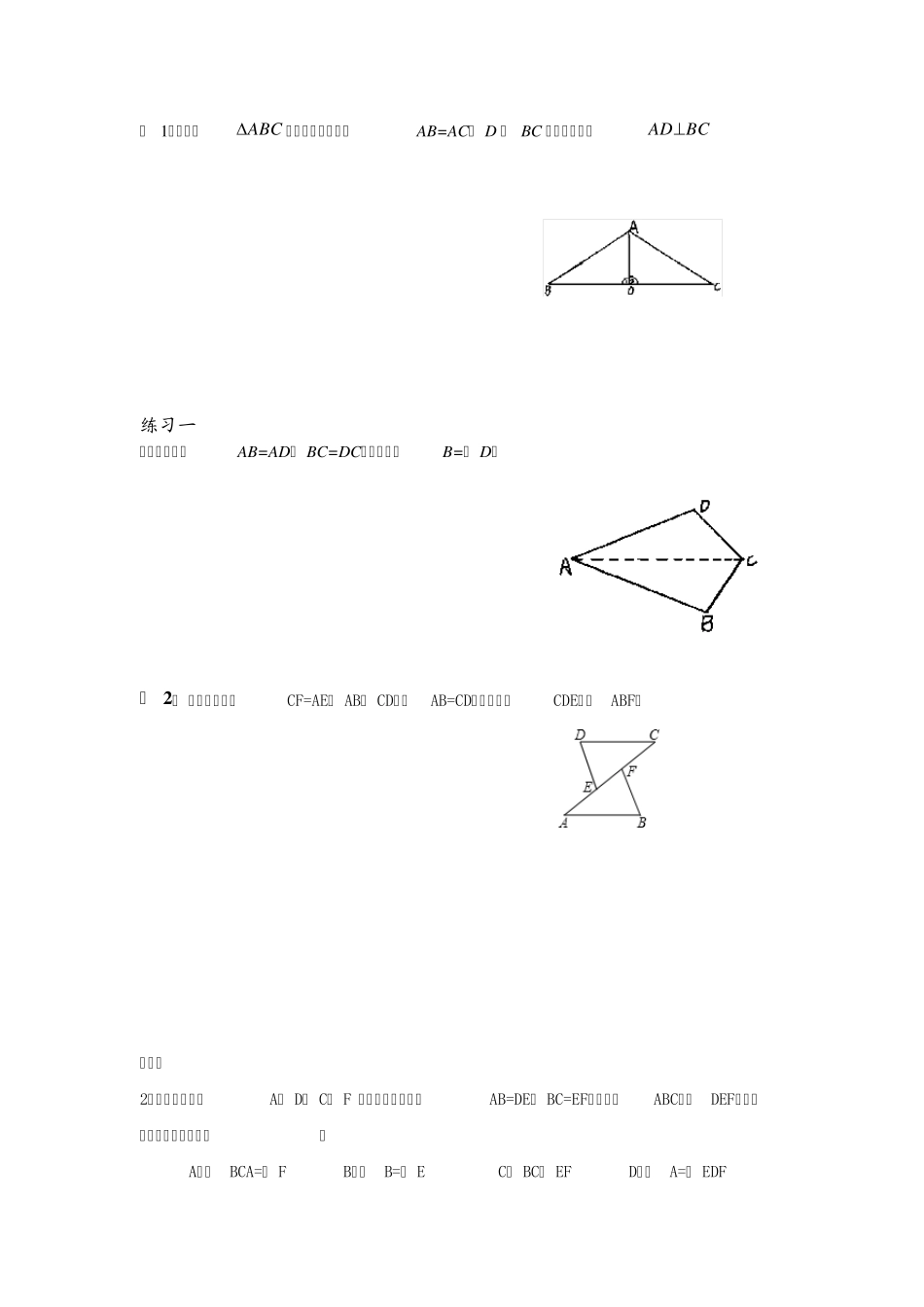
全等三角形的判定 知识要点 1、两个三角形全等的条件【重点】 ( 1)判定1——边边边公理 三边对应相等的两个三角形全等,简写成“边边边”或“SSS”。 “边边边”公理的实质:三角形的稳定性(用三根木条钉三角形木架)。 注意:边边边是三条边都相等,并且在书写时边与边要对应书写。在已知两边相等的情况下优先考虑。 ( 2)判定2——边角边公理 两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。 注意:边角边中,角是指两对应边的夹角,如上图中,同样在书写时对应边角对准。比如上图中正确的写法是:△ABC≌△A' B' C' ( 3)判定3——角边角公理 角和它们的夹边对应相等的两个三角形全等。简写为“角边角”或“ASA”。 注意:角边角中,边是两个角中间时,才能描述为角边角,否则就是下面的角角边。 ( 4)判定4——角角边推论 两角和其中一角的对边对应相等的两个三角形全等。简称“角角边”或“AAS”。 ( 5)直角三角形全等的判定——斜边直角边公理 斜边和一条直角边对应相等的两个直角三角形全等。简写成“斜边直角边”或“HL”。 判定直角三角形全等的方法: ①一般三角形全等的判定方法都适用; ②斜边-直角边公理 2、证明三角形全等一般有以下步骤: ( 1)读题:明确题中的已知和求证; ( 2)要观察待证的线段或角,在哪两个可能全等的三角形中 ( 3)、分析要证两个三角形全等,已有什么条件,还缺什么条件。有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角 ( 4)、先证明缺少的条件 ( 5)、再证明两个三角形全等 (要符合书写步骤:先写在某两个三角形中、然后写条件,再写结论) 典例 例 1 :如图,ABC 是一个屋顶钢架,AB=AC, D 是 BC 中点。求证:ADBC 练习一 已知:如图,AB=AD, BC=DC。求证:∠B=∠ D。 例 2: 已知:如图,CF=AE, AB∥ CD,且AB=CD.求证:△CDE≌△ABF. 练习二 2、如图,已知点A、 D、 C、 F 在同一条直线上,AB=DE, BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( ) A.∠BCA=∠ F B.∠B=∠ E C. BC∥ EF D.∠A=∠ EDF 2、如图,已知∠1=∠ 2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( ) A. AB=AC B. DB=DC C.∠ADB=∠ ADC D.∠B=∠ C 例 3、如图,已知点E, C 在线段BF 上,BE=...