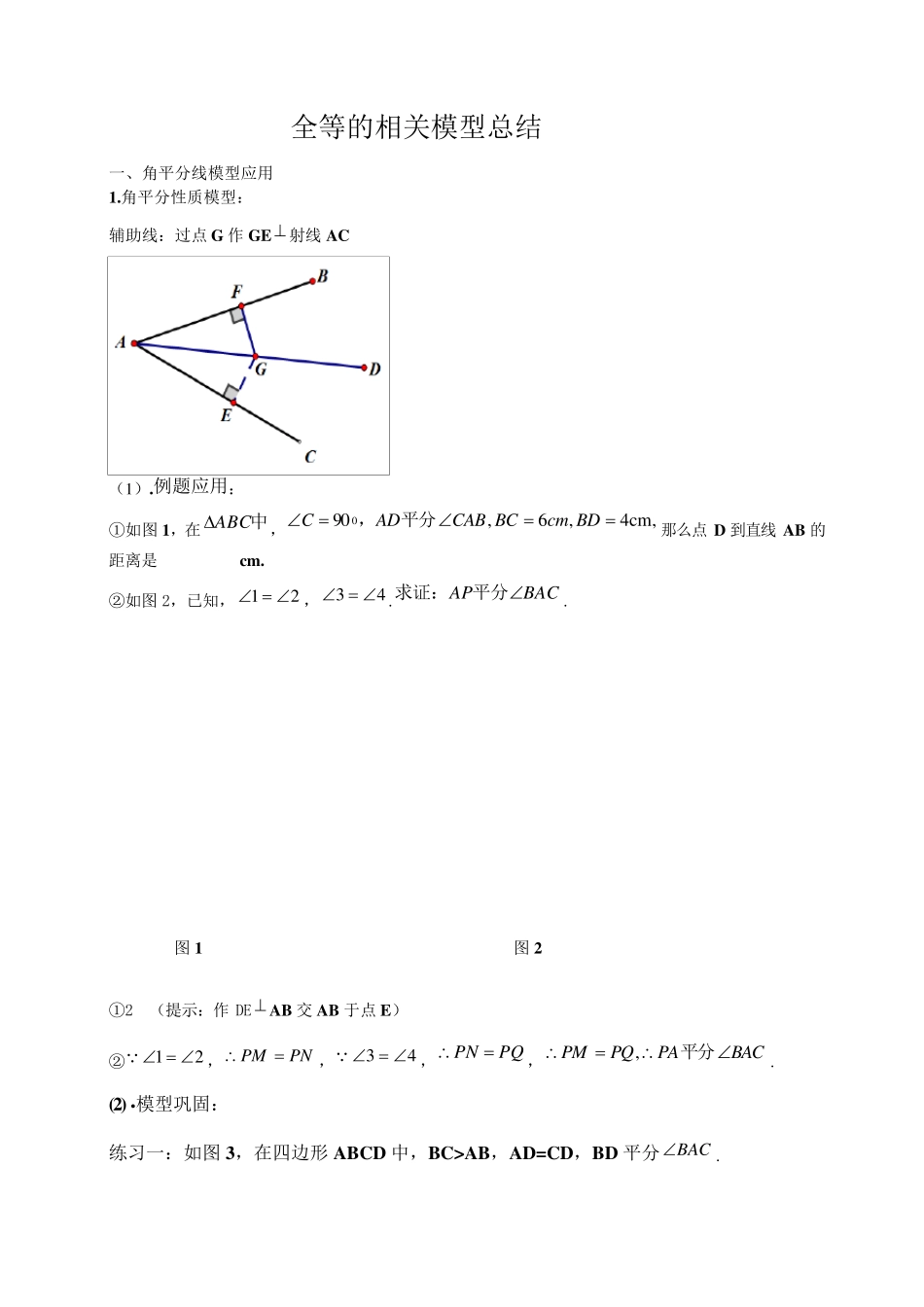
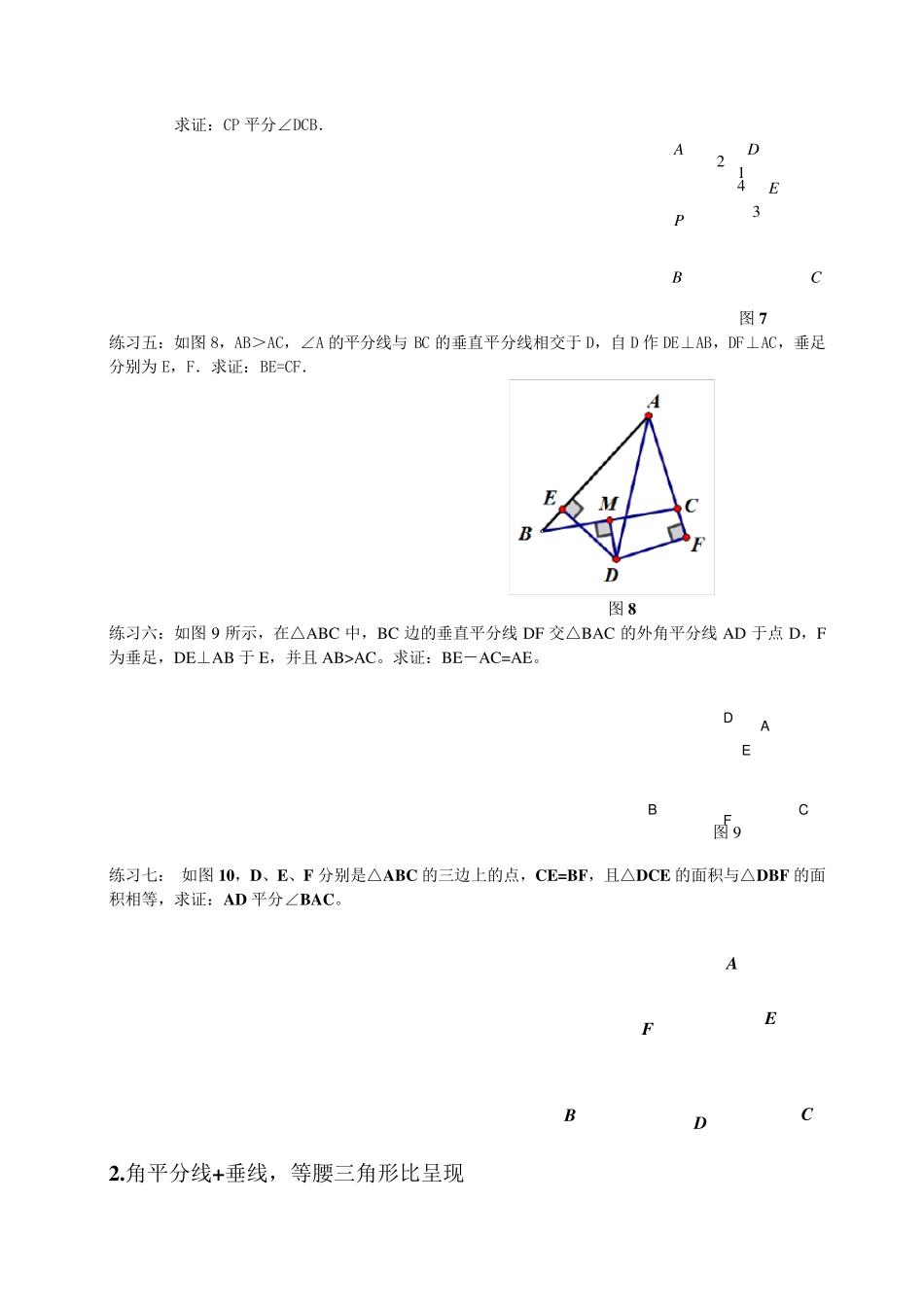
全等的相关模型总结 一、角平分线模型应用 1.角平分性质模型: 辅助线:过点G 作GE 射线AC (1).例题应用: ①如图 1,在中ABC,,cm4,6,90 0BDcmBCCABADC平分,那么点D 到直线AB 的距离是 cm . ②如图 2,已知,21,43.BACAP平分求证:. 图 1 图 2 ①2 (提示:作DE AB 交 AB 于点E) ②21,PNPM ,43,PQPN ,BACPAPQPM平分,. (2) .模型巩固: 练习一:如图 3,在四边形 ABCD 中,BC>AB,AD=CD,BD 平分BAC. .求证:1 8 0CA 图3 练习二:已知如图4,四边形ABCD 中, ..,1 8 0 0BADACCDBCDB平分求证: 图4 练习三:如图5,,,9 0 0CABAFDABCDACBABCRt平分,垂足为,中,交CD 于点E,交CB 于点F. (1)求证:CE=CF. (2)将图5 中的△ADE 沿AB 向右平移到'''EDA的位置,使点'E 落在BC 边上,其他条件不变,如图6 所示,是猜想:'BE 于CF 又怎样的数量关系?请证明你的结论. 图5 图6 练习四:如图7,9 0AADBC,∠∥,P 是AB 的中点,PD 平分∠ADC. 求证:CP 平分∠DCB. 图 7 练习五:如图 8,AB>AC,∠A 的平分线与 BC 的垂直平分线相交于 D,自 D 作 DE⊥AB,DF⊥AC,垂足分别为 E,F.求证:BE=CF. 图 8 练习六:如图 9 所示,在△ABC 中,BC 边的垂直平分线 DF 交△BAC 的外角平分线 AD 于点 D,F为垂足,DE⊥AB 于 E,并且 AB>AC。求证:BE-AC=AE。 练习七: 如图 10,D、E、F 分别是△ABC 的三边上的点,CE=BF,且△DCE 的面积与△DBF 的面积相等,求证:AD 平分∠BAC。 BCADEF 2.角平分线+垂线,等腰三角形比呈现 A D E C B P 2 1 4 3 FEDCBA图 9 辅助线:延长ED 交射线O B 于F 辅助线:过点E 作EF∥射线O B (1).例题应用: ①.如图1 所示,在△ABC 中,∠ABC=3∠C,AD 是∠BAC 的平分线,BE⊥AD 于F。 求证:1 ()2BEACAB 证明:延长BE 交AC 于点F。 ②.已知:如图2,在中ABC, ,,ADABDBCADBAC且于交的角平分线 )(21.ACABAMMADADCM求证:的延长线于交作 分析:此题很多同学可能想到延长线段CM ,但很快发现与要证明的结论毫无关系。而此题突破口就在于AB=AD,由此我们可以猜想过C 点作平行线来构造等腰三角形. 证明:过点C 作CE∥AB 交AM 的延长线于...