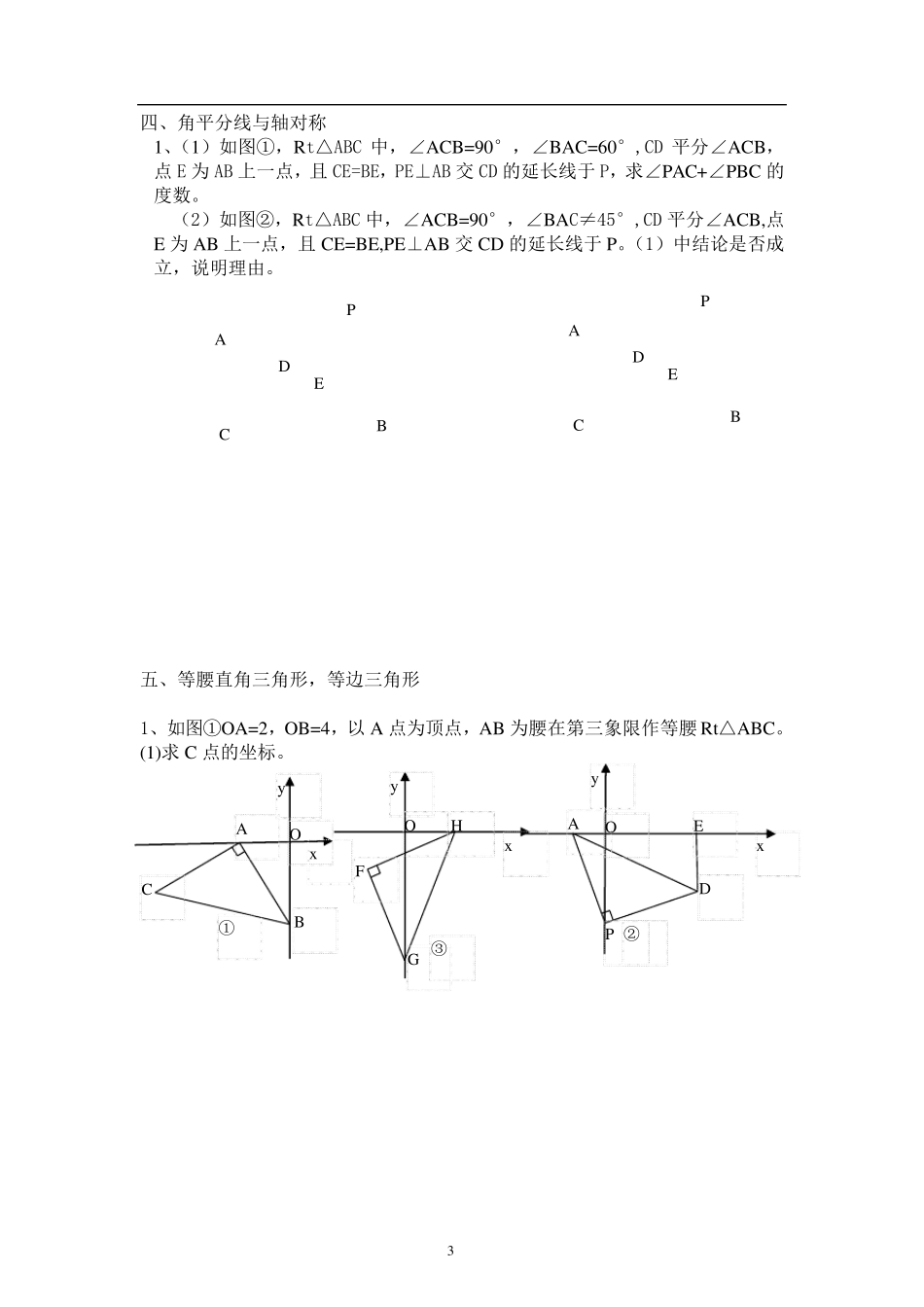
1 八年级数学上册辅助线专题 教学目标:掌握各种类型的全等三角形的证明方法 教学重点:构造全等三角形 教学难点: 如何巧妙作辅助线 知识点: (一)截长补短型 (二)中点线段倍长问题 (三)蝴蝶形图案解决定值问题 (四)角平分线与轴对称 (五)等腰直角三角形,等边三角形 (六)双重直图案与全等三角形 典型例题讲练 重点例题: 一、截长补短型 如图,RT△CDA ≌RT△CDB, ①、若∠ACD=30°,∠MDN=60°,当∠MDN 绕点D 旋转时,AM、MN、BN三条线段之间的关系式为______ ②、若∠ACD=45°,∠MDN=45°,AM、MN、BN 三条线段之间的数量关系式为:______ ③、由①②猜想:在上述条件下,当∠ACD 与∠MDN 满足什么条件时,上述关系式成立,证明你的结论。 二、中点线段倍长问题 如图△ABC 中,点D 是 BC 边中点,过点D 作直线交 AB、CA 延长线于点E、F。当 AE=AF 时,求证 BE=CF。 B A C D M N ① B D A C M N ② A B C D M N ③ A B C D E F 2 三、蝴蝶形图案解决定值问题 1、如图,在Rt△ACB 中,∠ACB=90°,CA=CB,D 是斜边 AB 的中点,E 是 DA上一点,过点 B 作 BH⊥CE 于点 H,交 CD 于点 F。 (1) 求证:DE=DF.(2)若 E 是线段 BA 的延长线上一点,其它条件不变,DE=DF 成立吗?画图说明。 2 在△ABC 中,AB=AC,AD 和 CE 是高,它们所在的直线相交于 H。 (1)如图1,若∠BAC=45°,求证:AH=2BD. (2)如图2,若∠BAC=135°,(1)中的结论是否依然成立?请你在图2 中画出图形并加以证明。 3,如图,等腰直角三角形ABC 中,AB=AC,∠BAC=90°,BE 平分∠ABC 交 AC于 E,过 C 作 CD⊥BE 于 D.求证 BE=2CD. (2) 连接 AD,求证:∠ADB=45°. A B C D E F H A B C D E H B A C C D B A E D B A E C 3 四、角平分线与轴对称 1、(1)如图①,Rt△ABC 中,∠ACB=90°,∠BAC=60°,CD 平分∠ACB,点 E 为 AB 上一点,且 CE=BE,PE⊥AB 交 CD 的延长线于 P,求∠PAC+∠PBC 的度数。 (2)如图②,Rt△ABC 中,∠ACB=90°,∠BAC≠45°,CD 平分∠ACB,点E 为 AB 上一点,且 CE=BE,PE⊥AB 交 CD 的延长线于 P。(1)中结论是否成立,说明理由。 五、等腰直角三角形,等边三角形 1、如图①OA=2,OB=4,以 A 点为顶点,AB 为腰在第三象限作等腰 Rt△ABC。(1)求 ...