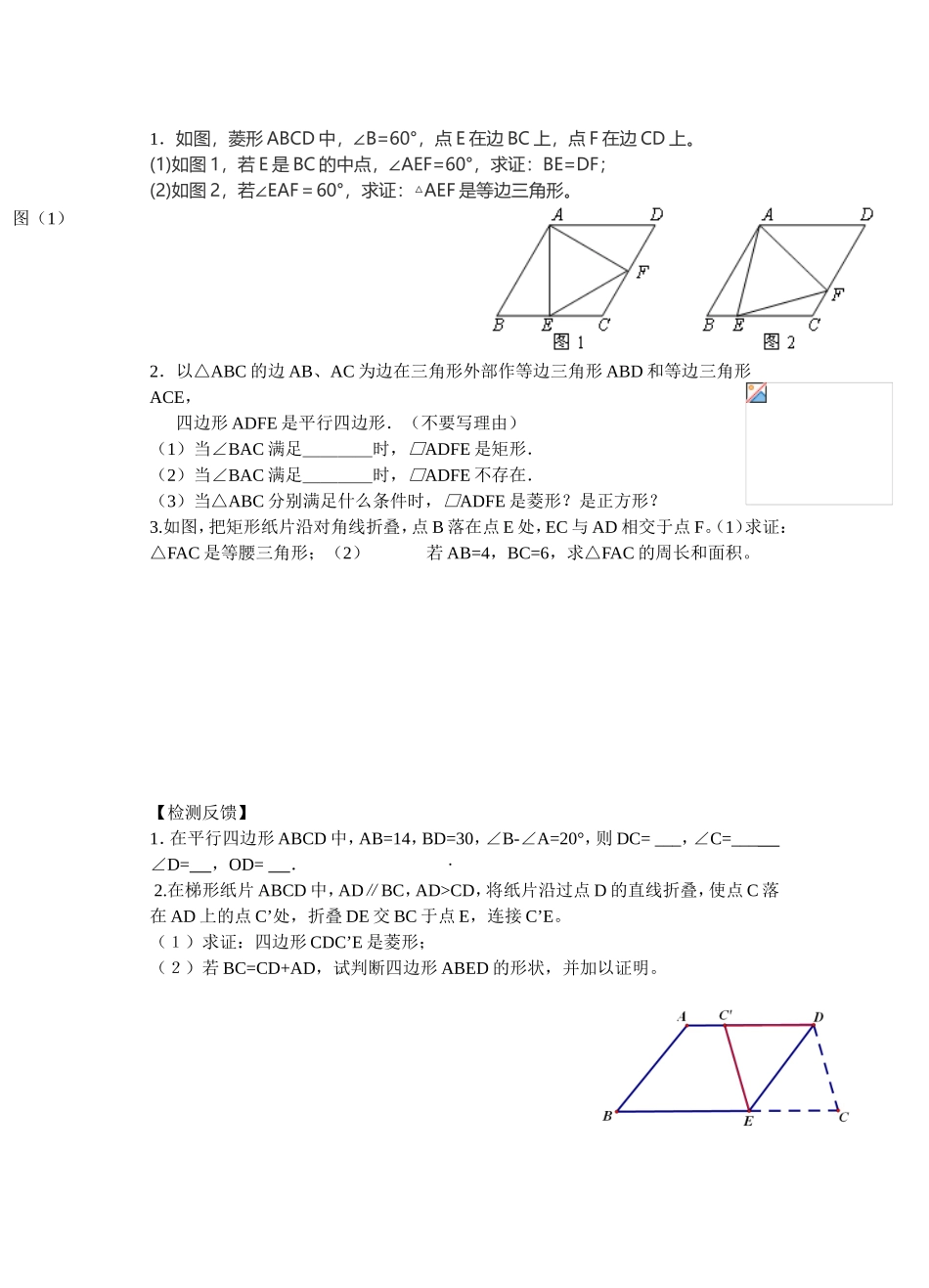
课题:四边形复习学习目标1.通过对几种特殊平行四边形的回顾与思考,梳理所学的知识.2.系统地复习特殊四边形的基本性质和常见判别方法.3.知道四边形与特殊四边形之间的关系及转化条件,在反思和交流过程中,逐渐建立知识体系.教学过程活动一以题理知1.在平行四边形ABCD中,若∠C=∠B+∠C,则∠A=度,∠B=度。2.已知平行四边形ABCD中,A、B、C三点的坐标是(-1,-1),(5,-1),(3,5),则D的坐标为3.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为4.如图,四边形ABCD是菱形,对角线AC=8厘米,BD=6厘米,DH垂直AB于H,则DH=5.如图,在▱ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EFAB⊥,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是小组交流:1.你在解这些题时用到了与四边形有关的哪些知识?有哪些注意点?2.请在箭头上方填上相应的条件(填一个即可)矩形四边形平行四边形正菱形3.特殊四边形面积的计算:活动二用知得法1.如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上。(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形。2.以△ABC的边AB、AC为边在三角形外部作等边三角形ABD和等边三角形ACE,四边形ADFE是平行四边形.(不要写理由)(1)当∠BAC满足____时,□ADFE是矩形.(2)当∠BAC满足____时,□ADFE不存在.(3)当△ABC分别满足什么条件时,□ADFE是菱形?是正方形?3.如图,把矩形纸片沿对角线折叠,点B落在点E处,EC与AD相交于点F。(1)求证:△FAC是等腰三角形;(2)若AB=4,BC=6,求△FAC的周长和面积。【检测反馈】1.在平行四边形ABCD中,AB=14,BD=30,∠B-A=20°∠,则DC=___,∠C=___D=∠,OD=.·2.在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C’处,折叠DE交BC于点E,连接C’E。(1)求证:四边形CDC’E是菱形;(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明。图(1)