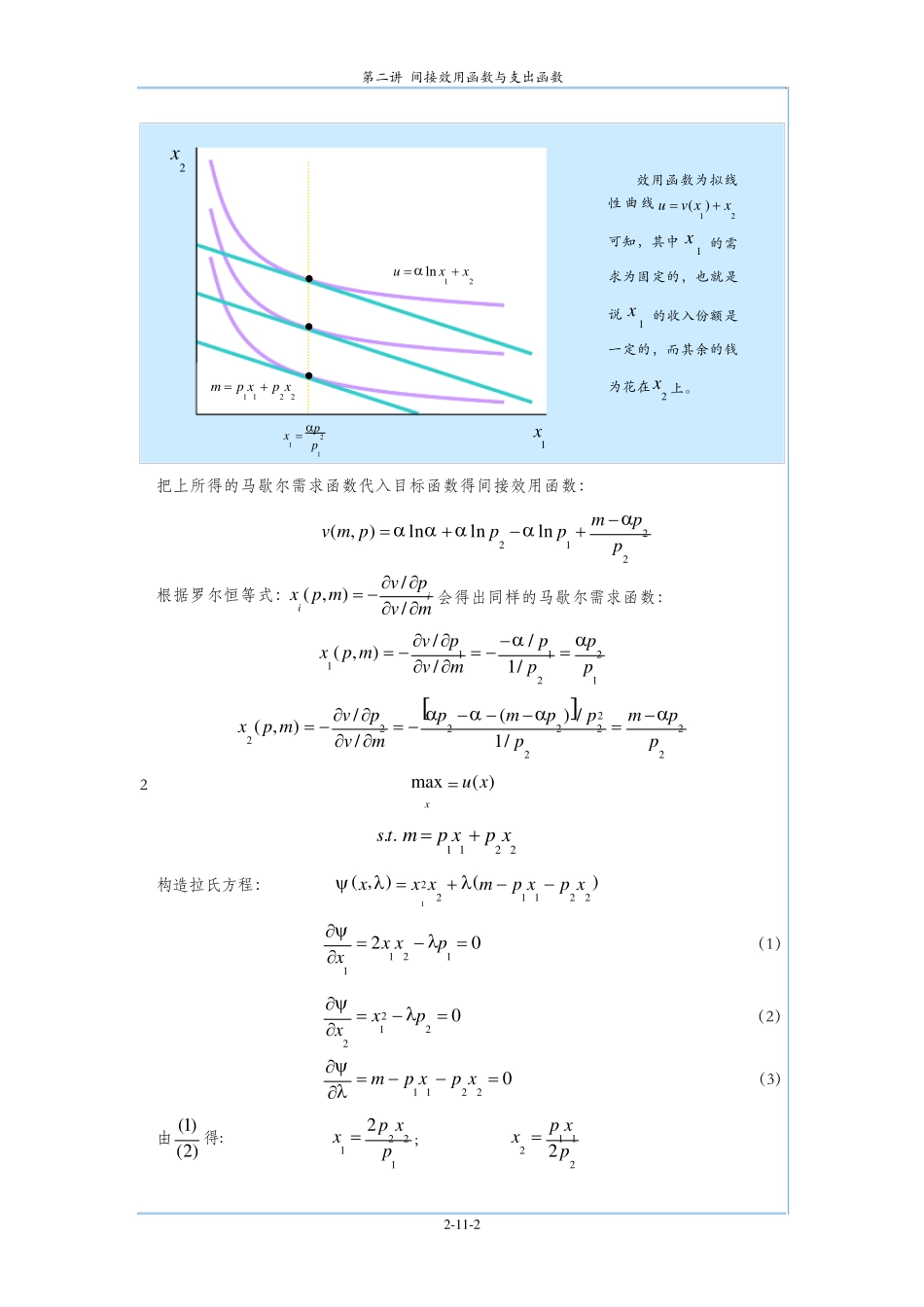
第 二 讲 间 接 效 用 函 数 与 支 出 函 数 第 二 讲 解 出 反 函 数 m 解 出 反 函 数 u 代 入),(upem = 代 入),(mpvu = 代 入 间 接 效 用 函 数 ( 支 出 函 数 ) 得 出 目 标 函 数 pxxmin )(..xuts )(maxxux mts .. 间 接 效 用 函 数 :),(mpv 支 出 函 数 :),(upe 希 克 斯 需 求 函 数 :),(uph 马 歇 尔 需 求 函 数 :),(mpx 谢 泼 特 引 理 : iipeuph∂∂=),( mvpvmpxii∂∂∂∂−=//),( 罗 尔 恒 等 式 : 代 入 目 标 函 数 代 入 目 标 函 数 1 )(maxxux ..ts2211xpxpm+= 构 造 拉 氏 方 程 : )(ln),(221121xpxpmxxx−−++=λαλψ 0111=−=∂∂pxxλαψ ( 1) 0122=−=∂∂pxλψ ( 2) 02211=−−=∂∂xpxpmλψ ( 3) 由 ( )( )21 得 马 歇 尔 需 求 函 数 : 121ppxα=; 因 为为 常 数 , 把 之 代 入 ( 3) 式 得 : 1x222ppmxα−= 2-11-1 第 二 讲 间 接 效 用 函 数 与 支 出 函 数 1x2x21lnxxu+= α2211xpxpm+=121ppxα= 效用函数为拟线性曲线21)(xxvu+=可 知 , 其 中1x的 需求 为 固 定 的 , 也 就 是说1x的 收 入 份 额 是一 定 的 , 而 其 余 的 钱为 花 在2x 上 。 • • • 把上所得的马歇尔需求函数代入目标函数得间接效用函数: 2212lnlnln),(ppmpppmvααααα−+−+= 根据罗尔恒等式:mvpvmpxii∂∂∂∂−=//),(会得出同样的马歇尔需求函数: 122111/1///),(ppppmvpvmpxαα=−−=∂∂∂∂−= []222222222/1/)(//),(ppmpppmpmvpvmpxαααα−=−−−−=∂∂∂∂−= 2 )(maxxux= ..ts2211xpxpm+= 构 造 拉 氏 方 程 : )(),(2211221xpxpmxxx−−+=λλψ 021211=−=∂∂pxxxλψ (1) 02212=−=∂∂pxxλψ (2) 02211=−−=∂∂xpxpmλψ ( 3) 由)2()1(得 : 12212pxpx =; 21122pxpx = 2-11-2 第 二 讲 间 接 效 用 函 数 与 支 出 函 数 把 上 两 式 分 别 代 入 ( 3) 式 得 马 歇 尔 需 求 函 数 : 1132),(pmmpx=; 223),(pmmpx= 把 上 所 得 的 马 歇 尔 需 求 函 数 代 入 目 标 函 数 得 间 接 效 用 函 数 : 2213334),(ppmmpv= 2211minxpxpx+ ..ts 22...