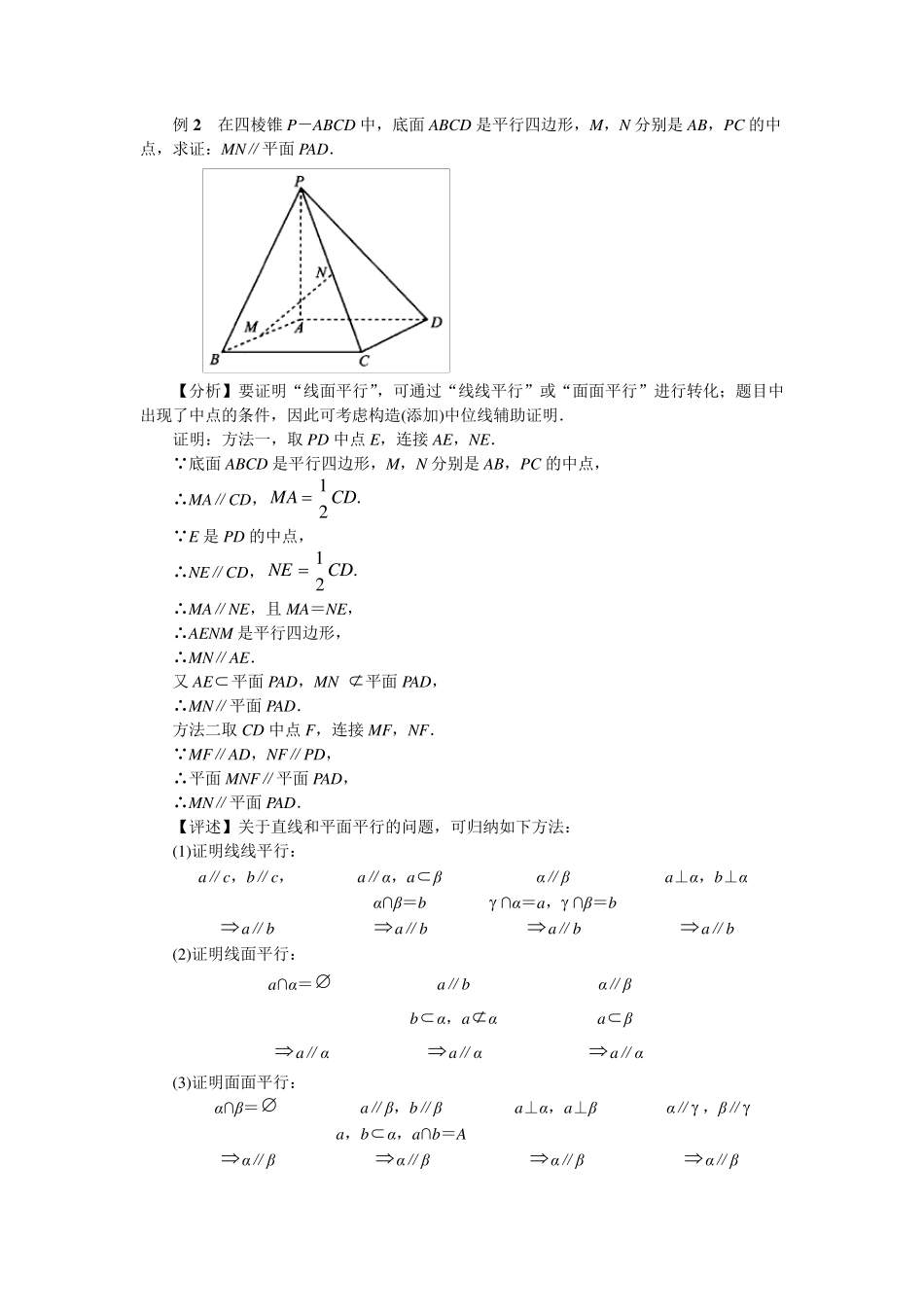
必修二立体几何典型例题 【知识要点】 1 .空间直线和平面的位置关系: (1 )空间两条直线: ①有公共点:相交,记作:a∩b=A,其中特殊位置关系:两直线垂直相交. ②无公共点:平行或异面. 平行,记作:a∥b. 异面中特殊位置关系:异面垂直. (2 )空间直线与平面: ①有公共点:直线在平面内或直线与平面相交. 直线在平面内,记作:a . 直线与平面相交,记作:a∩=A,其中特殊位置关系:直线与平面垂直相交. ②无公共点:直线与平面平行,记作:a∥. (3 )空间两个平面: ①有公共点:相交,记作:∩=l,其中特殊位置关系:两平面垂直相交. ②无公共点:平行,记作:∥. 2 .空间作为推理依据的公理和定理: (1 )四个公理与等角定理: 公理 1 :如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内. 公理 2 :过不在一条直线上的三点,有且只有一个平面. 公理 3 :如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 公理 4 :平行于同一条直线的两条直线互相平行. 定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. (2 )空间中线面平行、垂直的性质与判定定理: ①判定定理: 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行. 如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行. 如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直. 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直. ②性质定理: 如果一条直线与一个平面平行,那么经过该直线的任一个平面与此平面的交线与该直线平行. 如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.垂直于同一个平面的两条直线平行. 如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直. (3 )我们把上述判定定理与性质定理进行整理,得到下面的位置关系图: 【例题分析】 例2 在四棱锥P-ABCD 中,底面ABCD 是平行四边形,M,N 分别是AB,PC 的中点,求证:MN∥平面PAD. 【分析】要证明“线面平行”,可通过“线线平行”或“面面平行”进行转化;题目中出现了中点的条件,因此可考虑构造(添加)中位线辅助证明. 证明:方法一,取 PD 中点E,连接 AE,NE. 底面ABCD 是平行四边形,M,N...