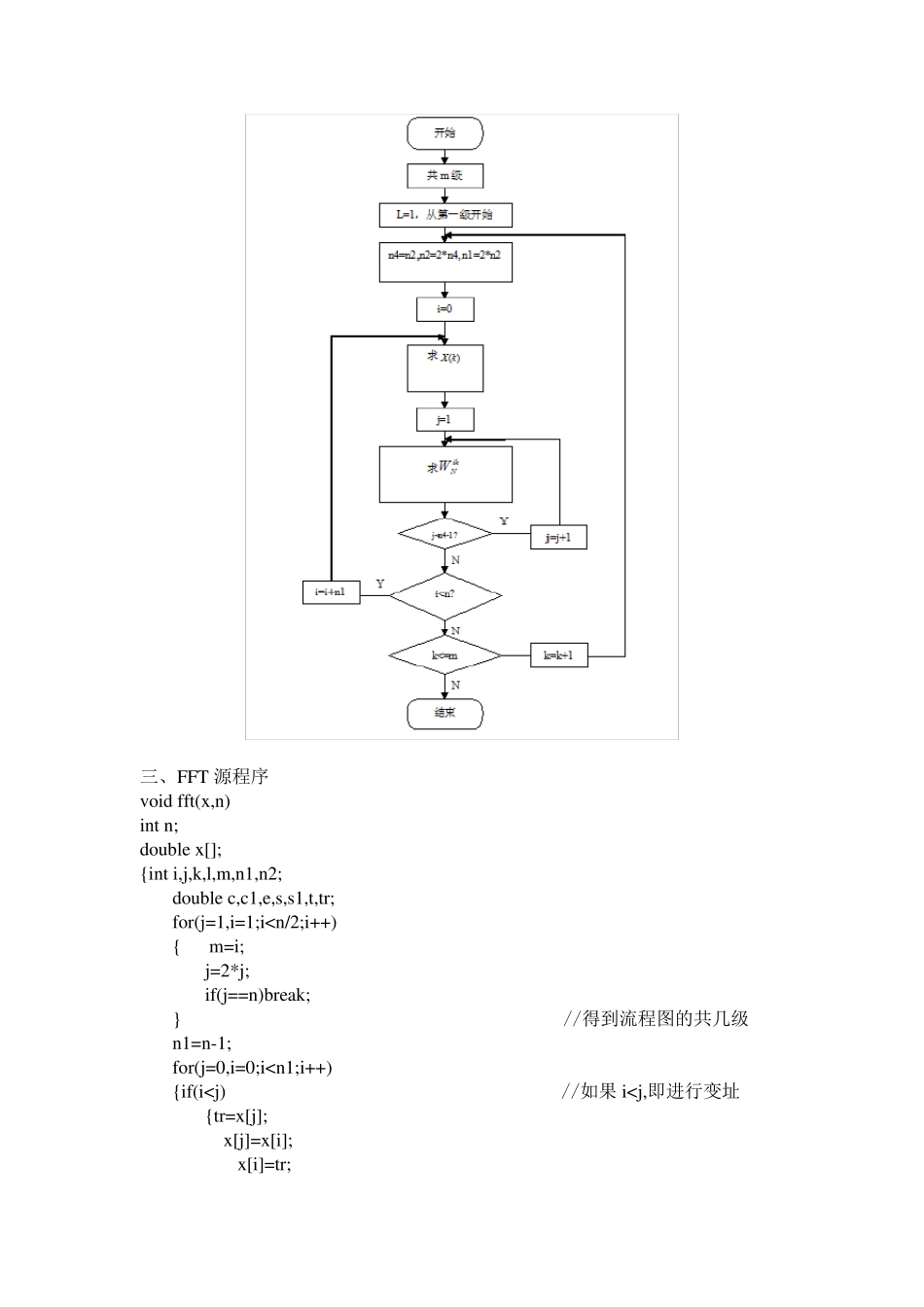
《测试信号分析及处理》课程作业 快速傅里叶变换 一、程序设计思路 快速傅里叶变换的目的是减少运算量,其用到的方法是分级进行运算。全部计算分解为M 级,其中NM2lo g;在输入序列ix中是按码位倒序排列的,输出序列 kX是按顺序排列;每级包含2N 个蝶形单元,第i 级有iN2个群,每个群有12 i 个蝶形单元; 每个蝶形单元都包含乘rNW 和rNW系数的运算,每个蝶形单元数据的间隔为12 i ,i 为第i 级; 同一级中各个群的系数W 分布规律完全相同。 将输入序列ix按码位倒序排列时,用到的是倒序算法——雷德算法。 自然序排列的二进制数,其下面一个数总比上面的数大 1,而倒序二进制数的下面一个数是上面一个数在最高位加 1 并由高位向低位仅为而得到的。 若已知某数的倒序数是J ,求下一个倒序数,应先判断 J 的最高位是否为0,与2Nk 进行比较即可得到结果。如果Jk ,说明最高位为0,应把其变成1,即2NJ ,这样就得到倒序数了。如果Jk ,即 J 的最高位为1,将最高位化为0,即2NJ ,再判断次高位;与4Nk 进行比较,若为0,将其变位1,即4NJ ,即得到倒序数,如果次高位为1,将其化为0,再判断下一位……即从高位到低位依次判断其是否为1,为1 将其变位0,若这一位为0,将其变位1,即可得到倒序数。若倒序数小于顺序数,进行换位,否则不变,防治重复交换,变回原数。 注:因为0 的倒序数为0,所 以 可从1 开 始 进行求解。 二、程序设计框 图 ( 1) 倒序算法——雷德算法流 程图 (2)FFT 算法流程 三、FFT 源程序 void fft(x,n) int n; double x[]; {int i,j,k,l,m,n1,n2; double c,c1,e,s,s1,t,tr; for(j=1,i=1;i