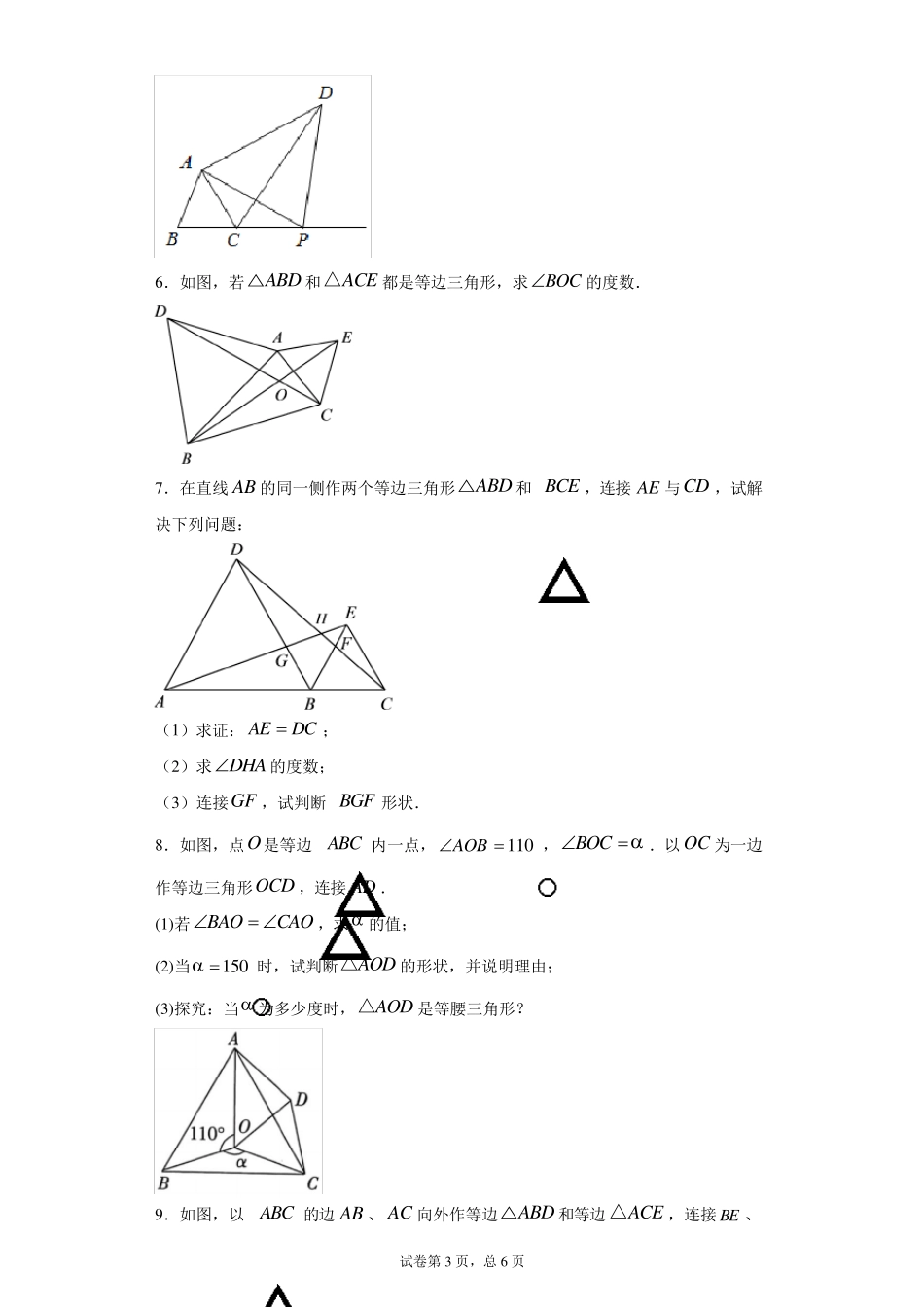
试卷第1 页,总6 页 手拉手模型专题训练 一、解答题 1 .(1 )如图①,ABC 和CDE△都是等边三角形,且点 B ,C ,E 在一条直线上,连结 BD 和 AE ,直线 BD ,AE 相交于点 P .则线段 BD 与 AE 的数量关系为_ _ _ _ _ _ _ _ _ _ _ _ _ .BD 与 AE 相交构成的锐角的度数为_ _ _ _ _ _ _ _ _ _ _ . (2 )如图②,点 B ,C ,E 不在同一条直线上,其它条件不变,上述的结论是否还成立. (3 )应用:如图③,点 B ,C ,E 不在同一条直线上,其它条件依然不变,此时恰好有3 0AEC.设直线 AE 交CD 于点Q ,请把图形补全.若2PQ ,则 DP _ _ _ _ _ _ _ _ _ _ _ . 2 .在 Rt ABC 中,9 0BAC,ABAC. (1 )如图1 ,点 D 为 BC 边上一点,连接 AD ,以 AD 为边作 Rt ADE△,9 0DAE ,ADAE,连接 EC .直接写出线段 BD 与CE 的数量关系为 ,位置关系为 . (2 )如图2 ,点 D 为 BC 延长线上一点,连接 AD ,以 AD 为边作 Rt ADE△,9 0DAE ,ADAE,连接 EC . ①用等式表示线段 BC ,DC ,EC 之间的数量关系为 . ②求证:2222BDCDAD. (3 )如图3 ,点 D 为ABC 外一点,且4 5ADC ,若1 3BD ,5CD ,求 AD的长. 试卷第2 页,总6 页 3.如图,在ABC中,D 是BC 边上一点,且,//,ADAB AE BCBADCAE ,连接,DE 交AC 于点F . (1)若65B,求C的度数. (2)若AEAC,则AD 平分BDE是否成立?判断并说明理由. 4.如图,ACB△和ECD 都是等腰直角三角形,,,CACB CDCEACB△的顶点A 在ECD 的斜边DE 上,连接BD . (1)求证:BDAE. (2)若3cm ,6cmAEAD,求AC 的长. 5.如图,P为等边ABC 的边BC 延长线上的一动点,以AP为边向上作等边APD△,连接CD . (1)求证:ABPACD≌△△; (2)当 PCAC时,求PDC的度数; (3)PDC与PAC有怎样的数量关系?随着点P位置的变化,PDC与PAC的数量关系是否会发生变化?请说明理由. 试卷第3 页,总6 页 6 .如图,若ABD△和ACE△都是等边三角形,求BOC的度数. 7 .在直线 AB 的同一侧作两个等边三角形ABD△和BCE ,连接 AE 与CD ,试解决下列问题: (1 )求证: AEDC; (2 )求DHA的度数; (3 )连接G...