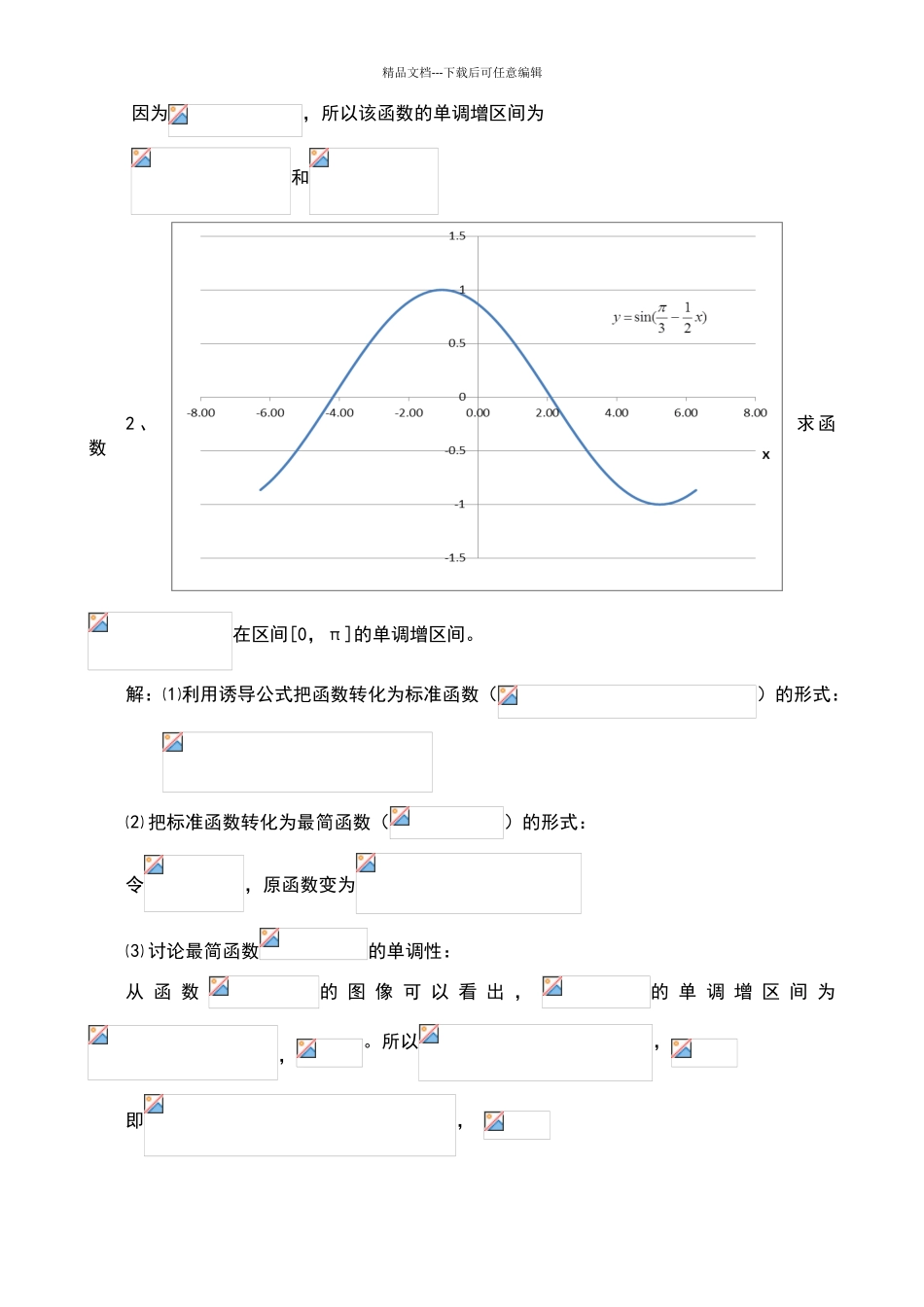
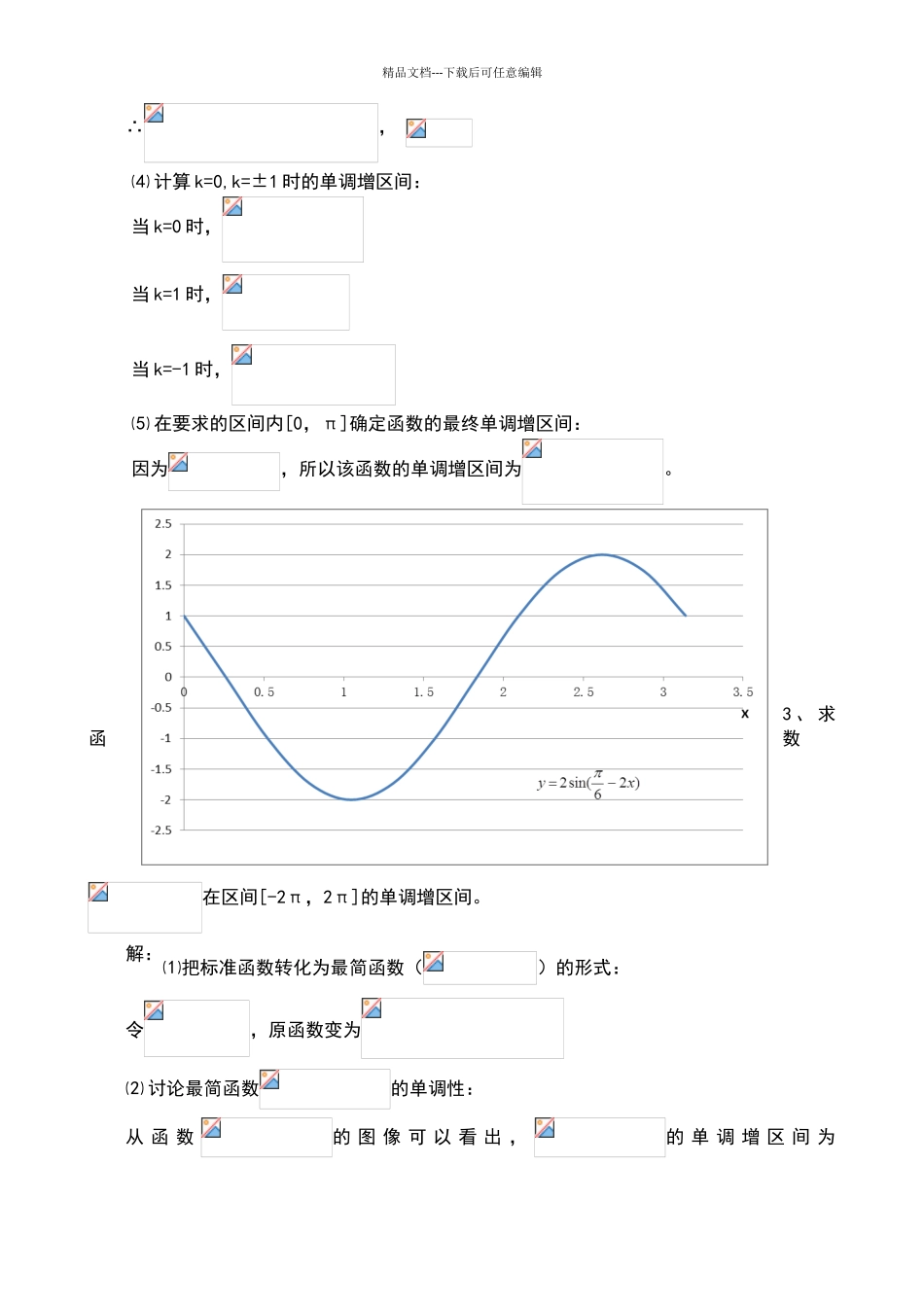
精品文档---下载后可任意编辑求三角函数的单调性的基本方法:函数的单调区间的确定,首先要看 A、ω 是否为正,若 ω为负,则先应用诱导公式化为正,然后将 ωx+φ 看作一个整体,化为最简式,再结合 A 的正负,在和两个区间内分别确定函数的单调增减区间。1、求函数在区间[-2π,2π]的单调增区间。解:⑴利用诱导公式把函数转化为标准函数()的形式:⑵ 把标准函数转化为最简函数()的形式:令,原函数变为⑶ 讨论最简函数的单调性:从 函 数的 图 像 可 以 看 出 ,的 单 调 增 区 间 为,。所以,即, ∴, ⑷ 计算 k=0,k=±1 时的单调增区间:当 k=0 时,当 k=1 时,当 k=-1 时,⑸ 在要求的区间内[-2π,2π]确定函数的最终单调增区间:精品文档---下载后可任意编辑因为,所以该函数的单调增区间为和2 、求函数在区间[0,π]的单调增区间。解:⑴利用诱导公式把函数转化为标准函数()的形式:⑵ 把标准函数转化为最简函数()的形式:令,原函数变为⑶ 讨论最简函数的单调性:从 函 数的 图 像 可 以 看 出 ,的 单 调 增 区 间 为,。所以,即, 精品文档---下载后可任意编辑∴, ⑷ 计算 k=0,k=±1 时的单调增区间:当 k=0 时,当 k=1 时,当 k=-1 时,⑸ 在要求的区间内[0,π]确定函数的最终单调增区间:因为,所以该函数的单调增区间为。3 、 求函数在区间[-2π,2π]的单调增区间。解:⑴把标准函数转化为最简函数()的形式:令,原函数变为⑵ 讨论最简函数的单调性:从 函 数的 图 像 可 以 看 出 ,的 单 调 增 区 间 为精品文档---下载后可任意编辑,。即, , ⑶ 计算 k=0,k=±1 时的单调增区间:当 k=0 时,当 k=1 时,当 k=-1 时,⑷ 在要求的区间内[-2π,2π]确定函数的最终单调增区间:又因为,所以该函数的单调增区间为-1.5-1-0.500.511.5-8-6-4-202468X精品文档---下载后可任意编辑4、求函数在区间[-π,π]的单调增区间解:⑴利用诱导公式把函数转化为标准函数()的形式:⑵ 把标准函数转化为最简函数()的形式:令,原函数变为⑶ 讨论最简函数的单调性:从函数的图像可以看出,的单调增区间为,;单调减区间为,。所以,单调增区间:,即, ∴, ① 计算 k=0,k=±1 时的单调增区间:当 k=0 时,当 k=1 时,当 k=-1 时,② 在要求的区间内[-π,π]确定函数的最终单调增区间:因为,所以该函数的单...