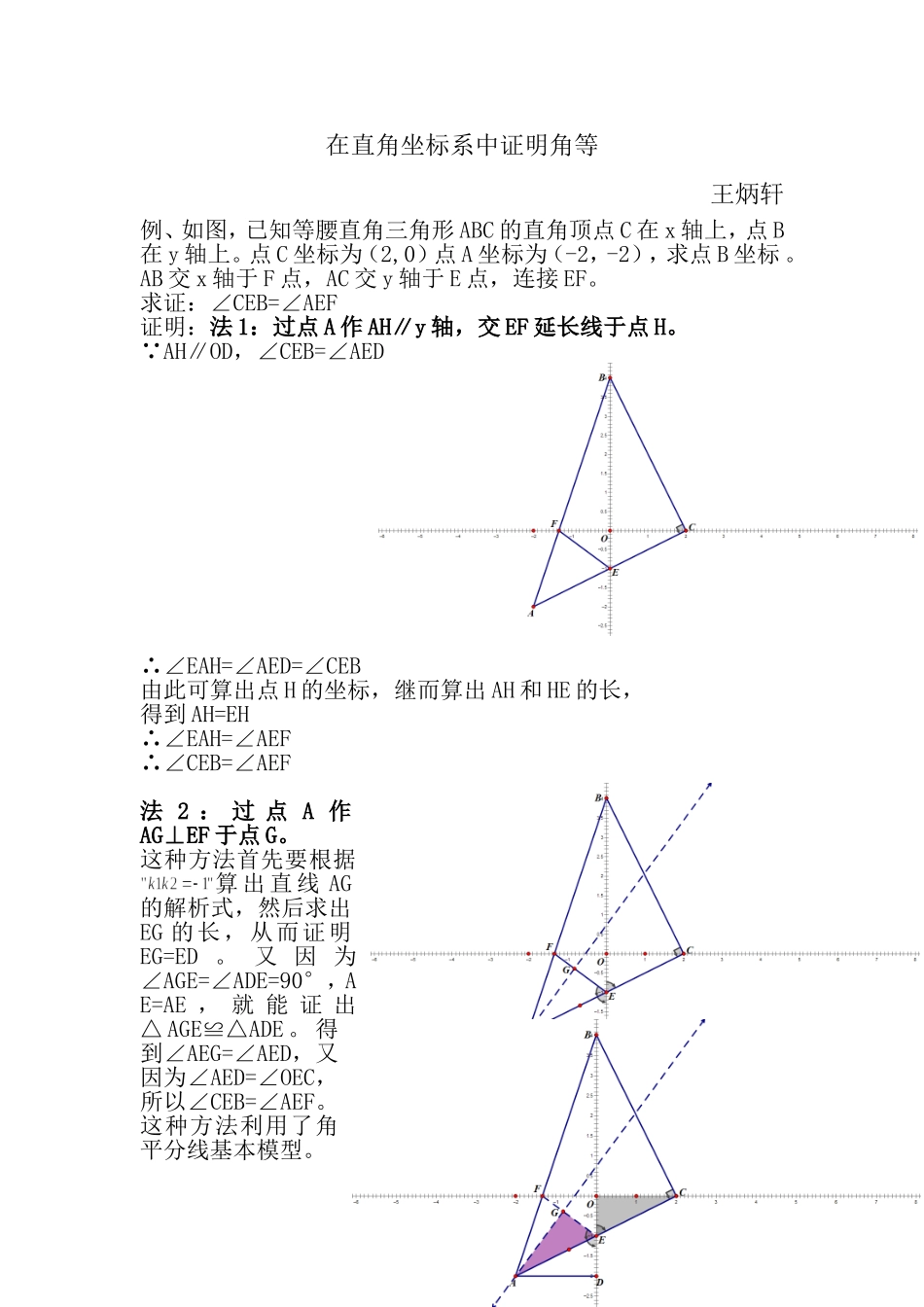
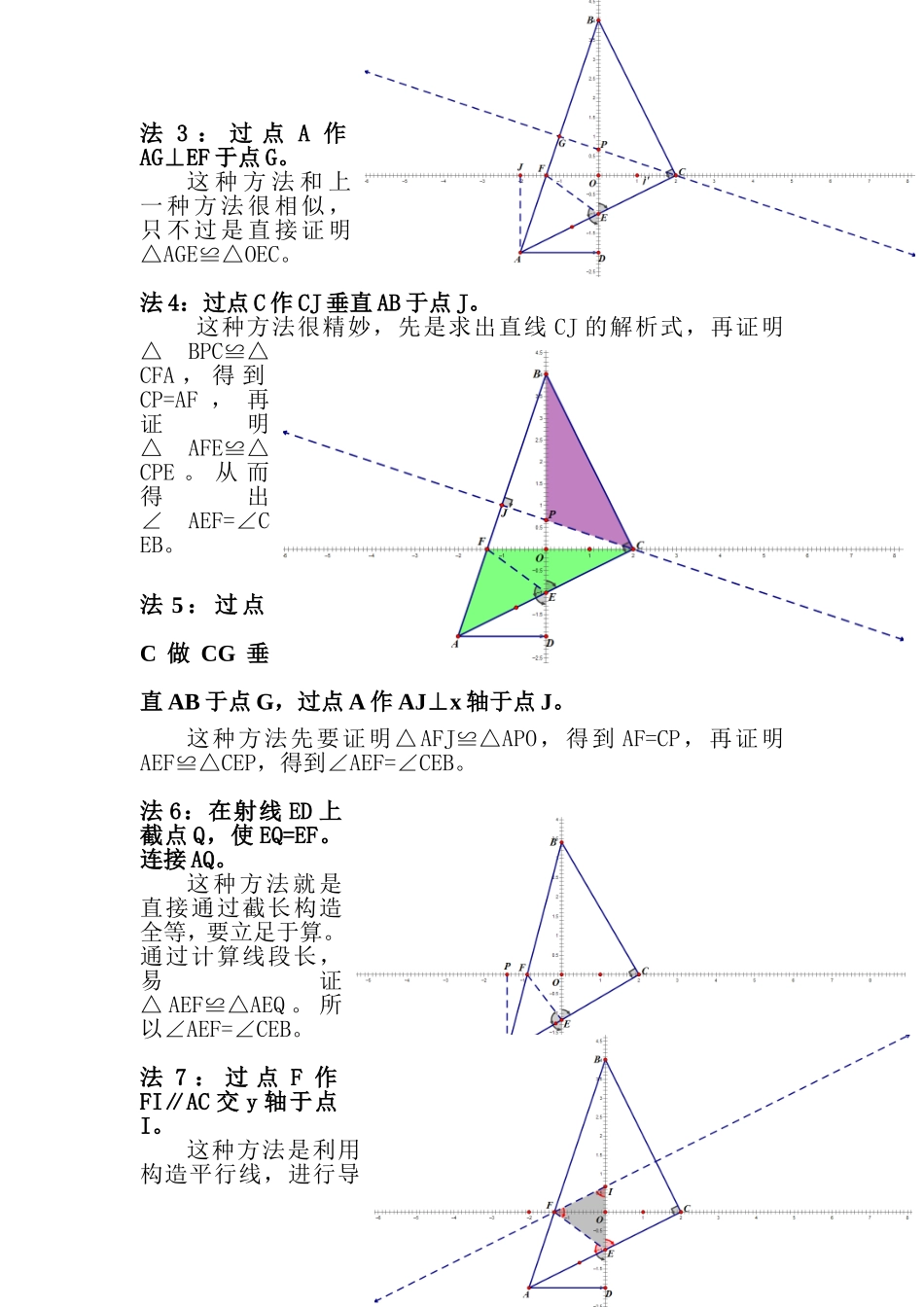
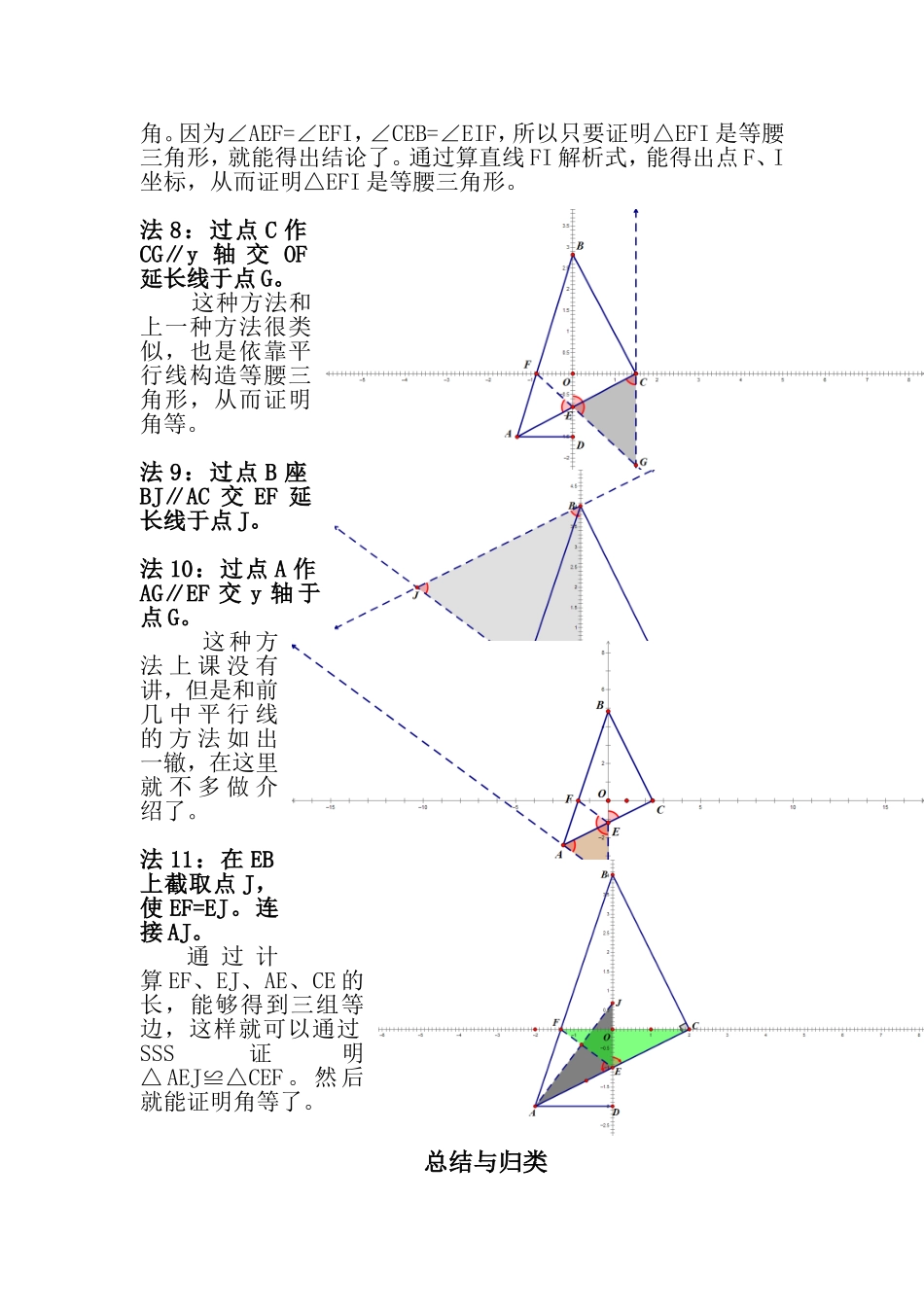
在直角坐标系中证明角等王炳轩例、如图,已知等腰直角三角形 ABC 的直角顶点 C 在 x 轴上,点 B在 y 轴上。点 C 坐标为(2,0)点 A 坐标为(-2,-2),求点 B 坐标 。AB 交 x 轴于 F 点,AC 交 y 轴于 E 点,连接 EF。求证:∠CEB=∠AEF证明:法 1:过点 A 作 AH∥y 轴,交 EF 延长线于点 H。 AH∥OD,∠CEB=∠AED∴∠EAH=∠AED=∠CEB由此可算出点 H 的坐标,继而算出 AH 和 HE 的长,得到 AH=EH∴∠EAH=∠AEF∴∠CEB=∠AEF法 2 : 过 点 A 作AG⊥EF 于点 G。这种方法首先要根据算 出 直 线 AG的解析式,然后求出EG 的长,从而证明EG=ED 。 又 因 为∠AGE=∠ADE=90°,AE=AE , 就 能 证 出△ AGE≌△ADE 。 得到∠AEG=∠AED,又因为∠AED=∠OEC,所以∠CEB=∠AEF。这种方法利用了角平分线基本模型。法 3 : 过 点 A 作AG⊥EF 于点 G。这 种 方 法 和 上一 种 方 法 很 相 似 ,只 不 过 是 直 接 证 明△AGE≌△OEC。法 4:过点 C 作 CJ 垂直 AB 于点 J。 这种方法很精妙,先是求出直线 CJ 的解析式,再证明△BPC≌△CFA , 得 到CP=AF , 再证明△AFE≌△CPE 。 从 而得出∠AEF=∠CEB。法 5 : 过 点C 做 CG 垂直 AB 于点 G,过点 A 作 AJ⊥x 轴于点 J。这种方法先要证明△AFJ≌△APO,得到 AF=CP,再证明AEF≌△CEP,得到∠AEF=∠CEB。法 6:在射线 ED 上截点 Q,使 EQ=EF。连接 AQ。 这种方法就是直接通过截长构造全等,要立足于算。通过计算线段长,易证△ AEF≌△AEQ 。 所以∠AEF=∠CEB。法 7 : 过 点 F 作FI∥AC 交 y 轴于点I。这种方法是利用构造平行线,进行导角。因为∠AEF=∠EFI,∠CEB=∠EIF,所以只要证明△EFI 是等腰三角形,就能得出结论了。通过算直线 FI 解析式,能得出点 F、I坐标,从而证明△EFI 是等腰三角形。法 8:过点 C 作CG∥y 轴 交 OF延长线于点 G。 这种方法和上一种方法很类似,也是依靠平行线构造等腰三角形,从而证明角等。法 9:过点 B 座BJ∥AC 交 EF 延长线于点 J。法 10:过点 A 作AG∥EF 交 y 轴 于点 G。 这种方法 上 课 没 有讲,但是和前几 中 平 行 线的 方 法 如 出一辙,在这里就 不 多 做 介绍了。法 11:在 EB上截取点 J,使 EF=EJ。连接 AJ。通 过 计算 EF、EJ、AE、CE 的长,能...