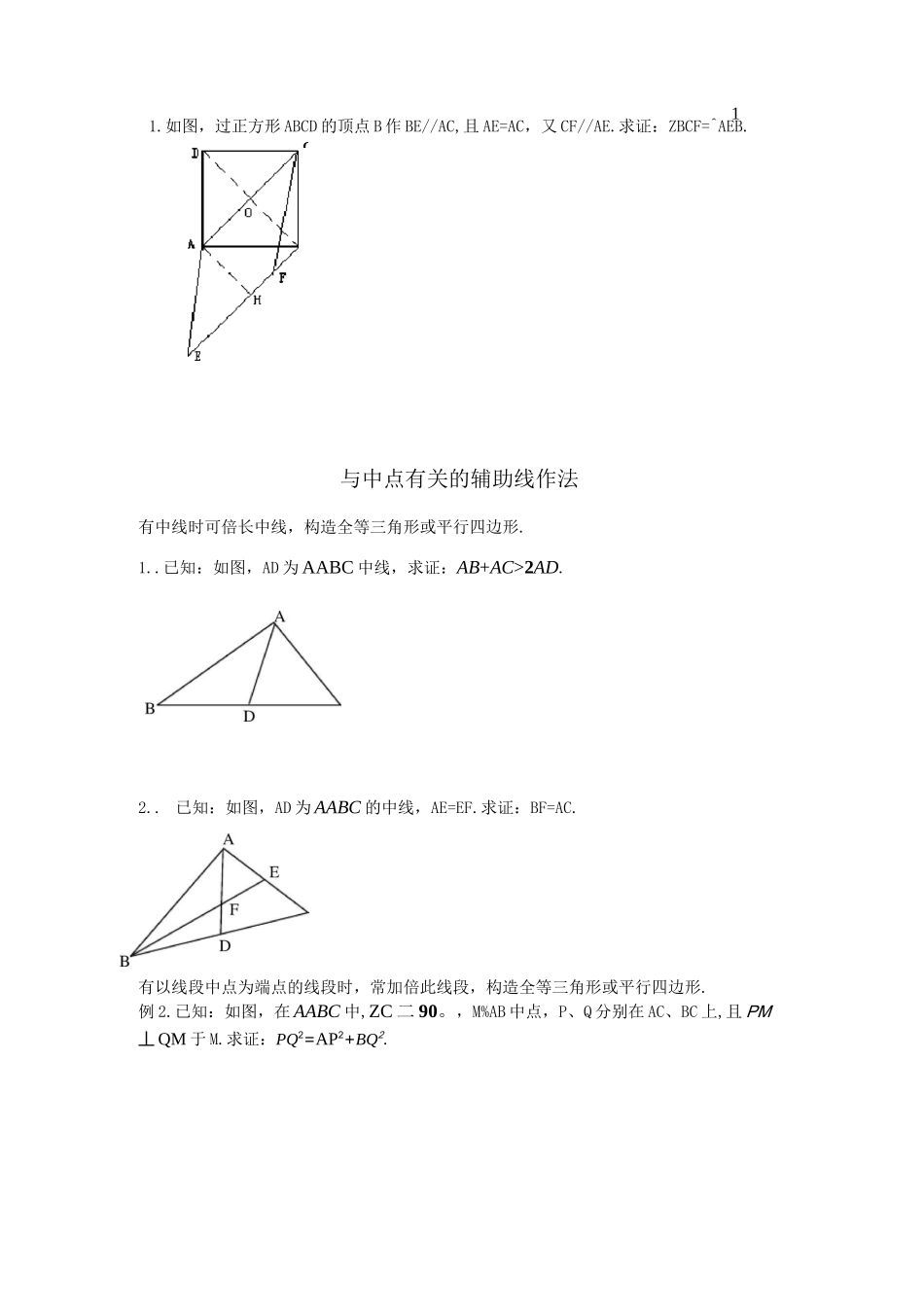
1平行四边形有关的辅助线作法1.利用一组对边平行且相等构造平行四边形例 1 如图 1,已知点 0 是平行四边形 ABCD 的对角线 AC 的中点,四边形 OCDE 是平行四边形.求证:OE 与 AD 互相平分.2.利用两组对边平行构造平行四边形例 2 如图 2,在 AABC 中,E、F 为 AB 上两点,AE=BF,ED//AC,FG//AC 交 BC 分别为 D,G.求证:ED+FG=AC.3.利用对角线互相平分构造平行四边形例 3 如图 3,已知人。是 4ABC 的中线,BE 交 AC 于 E,交 AD 于 F,且 AE=EF.求证 BF=AC.二、和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线,借助菱形的判定定理或性质定定理解决问题.图A2I#DF1.如图,在厶 ABC 中,ZACB=90°,ZBAC 的平分线交 BC 于点 D,E 是 AB 上一点,且AE=AC,EF//BC 交 AD 于点 F,求证:四边形 CDEF 是菱形.2.如图,四边形 ABCD 是菱形,E 为边 AB 上一个定点,F 是 AC 上一个动点,求证 EF+BF的最小值等于 DE 长.三、与矩形有辅助线作法和矩形有关的题型一般有两种:(1)计算型题,一般通过作辅助线构造直角三角形借助勾股定理解决问题;(2)证明或探索题,一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少.如图,已知矩形 ABCD 内一点,PA=3,PB=4,PC=5.求 PD 的长.四、与正方形有关辅助线的作法正方形是一种完美的几何图形,它既是轴对称图形,又是中心对称图形,有关正方形的试题较多•解决正方形的问题有时需要作辅助线,作正方形对角线是解决正方形问题的常用辅助线.11.如图,过正方形 ABCD 的顶点 B 作 BE//AC,且 AE=AC,又 CF//AE.求证:ZBCF=^AEB.与中点有关的辅助线作法有中线时可倍长中线,构造全等三角形或平行四边形.1..已知:如图,AD 为 AABC 中线,求证:AB+AC>2AD.2.. 已知:如图,AD 为 AABC 的中线,AE=EF.求证:BF=AC.有以线段中点为端点的线段时,常加倍此线段,构造全等三角形或平行四边形.例 2.已知:如图,在 AABC 中,ZC 二 90。,M%AB 中点,P、Q 分别在 AC、BC 上,且 PM丄 QM 于 M.求证:PQ2=AP2+BQ2.C有中点时,可连结中位线.1.已知:如图,E、F 分别为四边形 ABCD 的对角线中点,AB〉CD.求证:EF>斗(AB-CD).有底边中点,连中线,利用等腰三角形“三线合一”性质证题1.. 已知:如图,在 RtAABC 中,ABAC 二 90。,AB=AC,D 为 BC 边中点,P 为 BC...