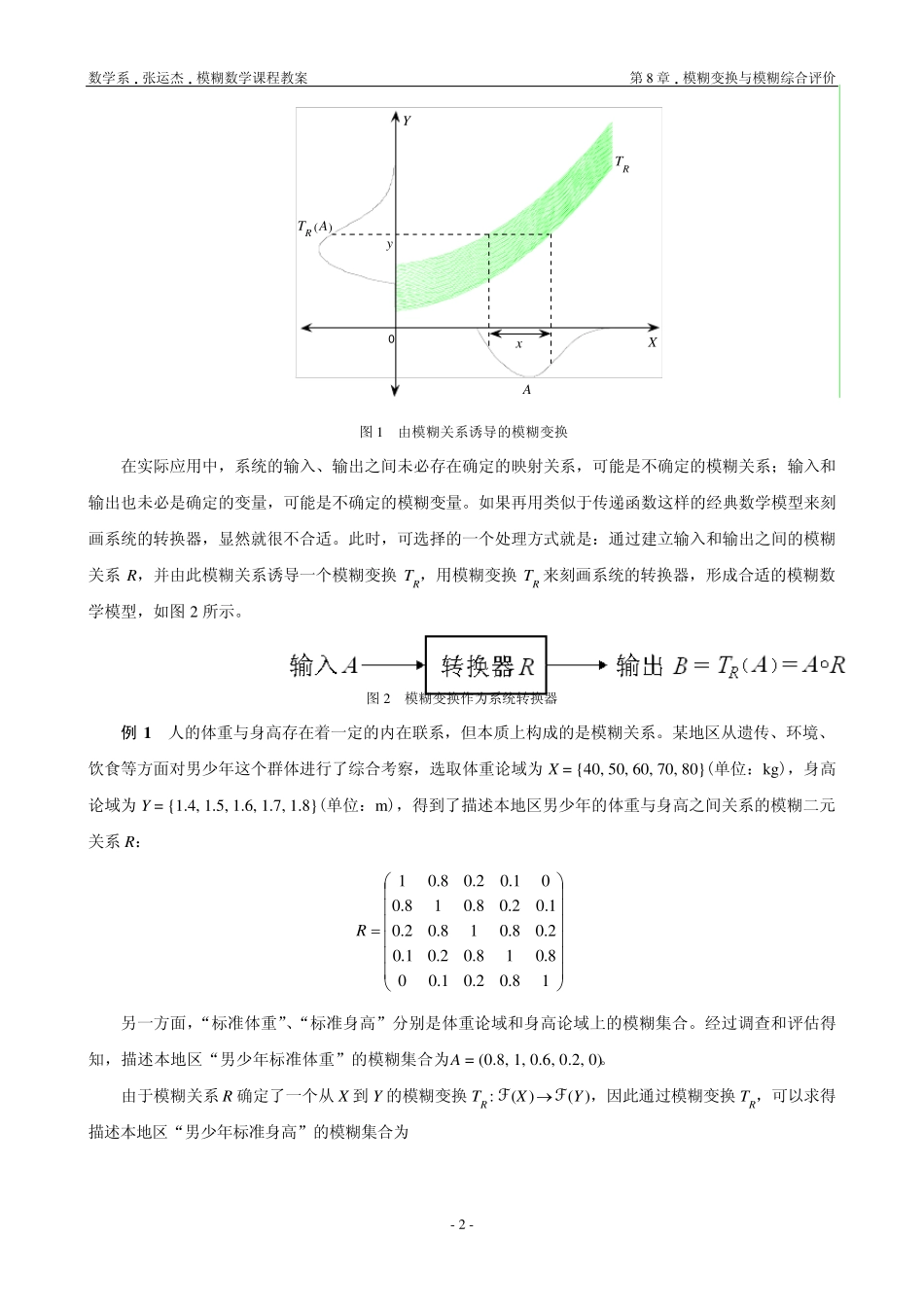
数 学 系 • 张 运 杰 • 模 糊 数 学 课 程 教 案 第 8 章 • 模 糊 变 换 与 模 糊 综 合 评 价 - 1 -第 8 章 模 糊 变 换 与 模 糊 综 合 评 价 模 糊 映 射 与 模 糊 变 换 , 是 建 立 在 模 糊 关 系 的 理 论 基 础 之 上 的 , 同 时 它 们 又 是 模 糊 综 合 评 价 和 模 糊 推 理的 理 论 基 础 。 本 章 主 要 介 绍 两 方 面 的 内 容 : 模 糊 映 射 与 模 糊 变 换 , 模 糊 综 合 评 价 方 法 。 8.1 模 糊 变 换 由 论 域 X 到 Y 的 点 映 射 f : X→Y 出 发 , 通 过 扩 张 原 理 , 可 以 扩 展 (诱 导 )出 一 个 从 F(X)到 F(Y)的 映 射f : F(X)→F(Y), 使 得 X 上 的 每 一 个 模 糊 集 合A 都 有 一 个Y 上 的 模 糊 集 合B 与 之 对 应 ; 也 可 以 扩 展 (诱 导 )出 一 个 从 F(Y)到 F(X)的 映 射 f : F(Y)→F(X), 使 得 Y 上 的 每 一 个 模 糊 集 合 B 都 有 一 个 X 上 的 模 糊 集 合 A与 之 对 应 。 实 际 上 , 我 们 还 可 以 一 般 性 地 讨 论 从 一 个 论 域 的 模 糊 幂 集 到 另 一 个 论 域 的 模 糊 幂 集 上 的 映 射 ,即 所 谓 的 模 糊 变 换 。 定义 1 设 X 和 Y 是 两 个 给 定 的 论 域 , 称 映 射 T: F(X)→F(Y) Aa B = T(A) (8.1) 为 从 论 域 X 到 论 域 Y 的 模糊变换; 称 B = T(A)为 A 在 模 糊 变 换 T 下 的 象, A 为 B 的 原象。 显 然 , 扩 张 原 理 将 X 到 Y 的 点 映 射 扩 展 成 为 X 到 Y 的 模 糊 变 换 。 在 经 典 集 合 论 中 , 映 射 与 二 元 关 系 有 着 很 强 的 内 在 联 系 : 映 射 描 述 的 是 两 集 合 之 间 有 限 定 条 件 的 对 应 ,二 元 关 系 描 述 是 两 集 合 之 间 不 加 限 定 的 对 应 , 映 射 是 特 殊 的 。 在 模 糊 集 合 论 中 , 模 糊 变 换 与 模 糊 二 元 关 系也 存 在 着 类 似的 情形, 只不 过 我 们 更关 心的 是 由...