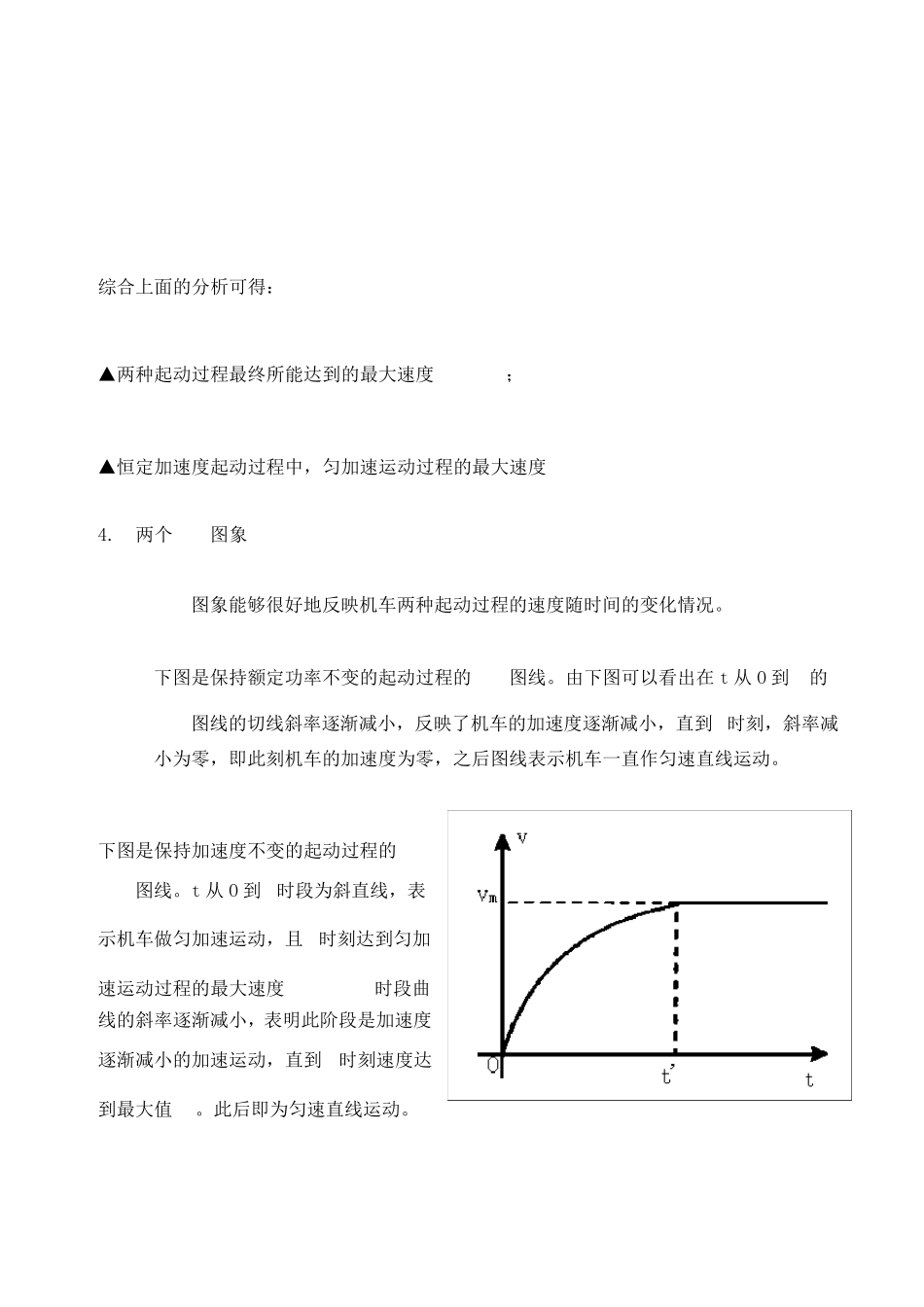
机 车 起 动 问 题 的 分析及处理策略 1. 两个起动方式 机车起动问题中有两种运动模式,即机车以恒定功率(通常为额定功率)和以恒定加速度a 起动。 如何分析这两种方式的起动过程及相关问题的处理,这是教与学中经常碰到的问题。 2. 两个基本关系 “”和“”是分析与处理机车起动过程的两个重要的、基本的关系式。它反映了机车瞬时状态的各量间的关系。 下图是机车在工作状态下的受力情况,应当明确 P 为机车的瞬时功率;F 为机车的牵引力,而不是机车受的合力;v 为机车的瞬时速度;a 为瞬时加速度;f 为机车所受的阻力(通常机车所受阻力设为恒力);m 是机车的质量。在实践中,我们只要抓住两个基本关系式,相关问题则会迎刃而解。 3. 两个最值速度 3.1 额定功率起动的情形 由和可知,因功率P 保持不变,速度增大,则机车的牵引力 F 必然减小,也就不难看出机车的加速度a 因此而减小,所以该过程是一个加速度逐渐减小的运动。显然当牵引力 F 减小到等于机车所受阻力 f 时,即F=f,其加速度a=0,则机车的速度达到最大值。 如下图所示,额定功率下起动过程的两个阶段,即从为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。 3.2 恒定加速度起动的情形 初速度为0 的匀加速起动的过程,同样根据知,由于加速度a 恒定,则牵引力 F 不变(通常设定机车所受阻力 f 恒定)。因此随着速度v 增大,其机车的瞬时功率P 随之增大,当 P 增大到额定功率时,此刻速度便是匀加速运动过程的最大速度,其大小为。 应当注意到是匀加速运动的末状态,此刻机车的功率刚好等于额定功率,而此时此刻牵引力仍为F,且 F,再由两个基本关系式,容易分析出,在功率不变的情况下,速度还会继续增大,牵引力随之减小,所以此后过程是加速度逐渐减小的加速运动,直到加速度时,机车的速度达到最终的最大速度。 如下图所示,恒定加速度起动的过程的三个阶段,即从为匀加速运动阶段;为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。 综合上面的分析可得: ▲两种起动过程最终所能达到的最大速度; ▲恒定加速度起动过程中,匀加速运动过程的最大速度 4. 两个图象 图象能够很好地反映机车两种起动过程的速度随时间的变化情况。 下图是保持额定功率不变的起动过程的图线。由下图可以看出在 t 从 O 到的图线的切线斜率逐渐减小,反映了机车的加速度逐渐减小,直到 时刻,斜率减小为零,即此刻机...