材料力学(金忠谋)第六版答案第01章

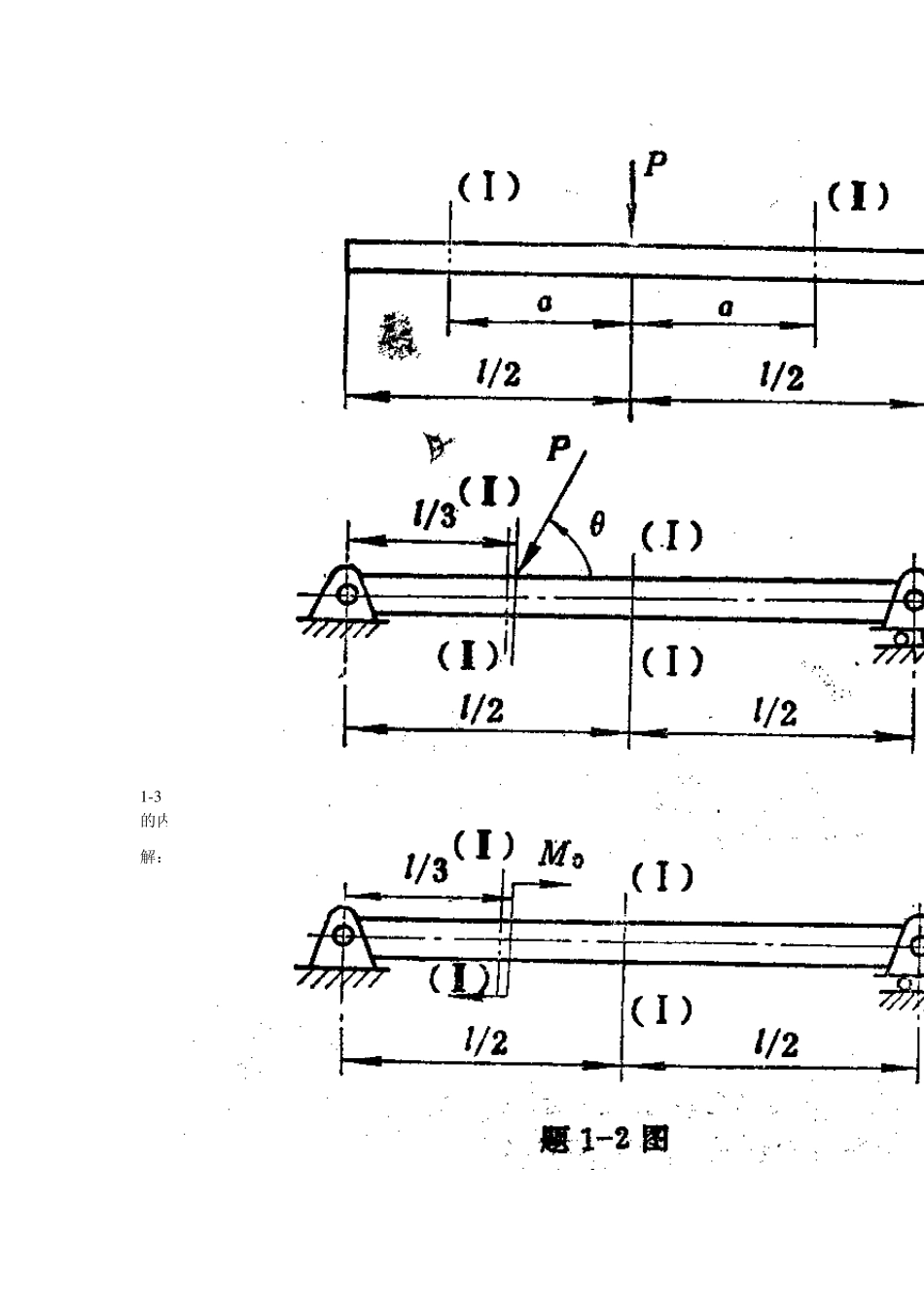
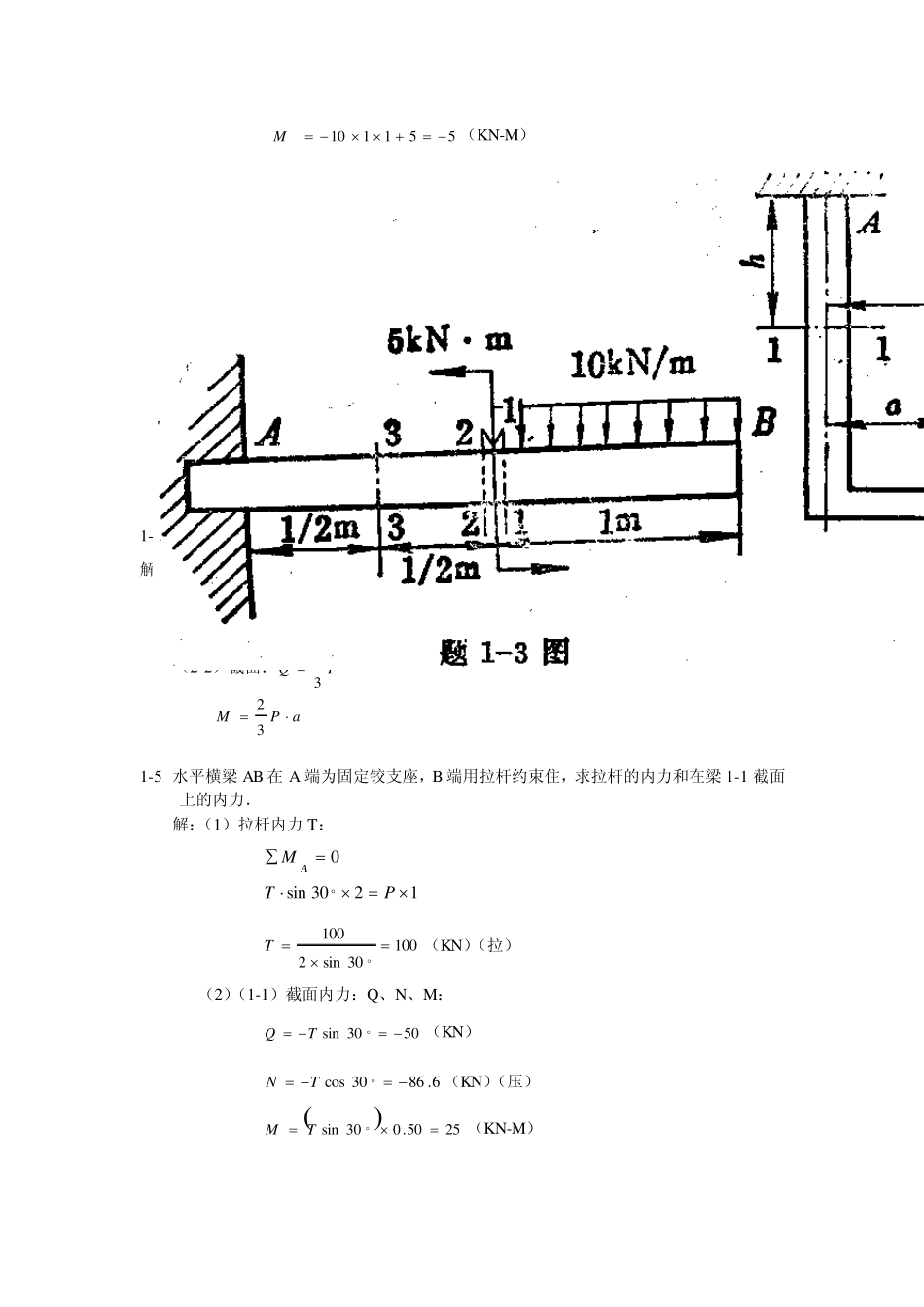
第一章 绪论 1-1 求图示杆在各截面（I）、（II）、（III）上的内力，并说明它的性质． 解：（a）I-I 截面： N = 20KN (拉) II-II 截面： N = -10KN （压） III-III 截面： N = -50KN (压) （b）I-I 截面： N = 40KN （拉） II-II 截面： N = 10KN (拉) III-III 截面： N = 20KN （拉） 1-2 已知P、M0、l、a，分别求山下列图示各杆指定截面（I）、(II)上的内力 解：（a）：（I）截面：内力为零。 （II）截面：M = Pa （弯矩） Q = -P （剪力） （b）：（I）截面：sin31 PQ  s i n61 PLM  （II）截面：sin32 PQ  s i n92 PLM  （c）：（I）截面：LMQ0 021 MM  （II）截面：LMQ0 031 MM  1-3 图示AB 梁之左端固定在墙内，试求（1）支座反力，（2）1-1、2-２、3-3 各横截面上的内力（1-1，2-2 是无限接近集中力偶作用点．） 解：10110AY（KN） 1055.110AM（KN-M） （1-1） 截面：10110Q（KN） 521110M（KN-M） （2-2）截面：10Q（KN） 055M（KN-M） （2-3）截面：10Q（KN） 551110M（KN-M） 1-4 求图示挂钩AB在截面 1-1、2-2上的内力． 解：（1-1）截面：PN32 aPM43 （2-2）截面：PQ32 aPM32 1-5 水平横梁 AB 在A 端为固定铰支座，B 端用拉杆约束住，求拉杆的内力和在梁 1-1 截面上的内力． 解：（1）拉杆内力 T： 1230sin0PTMA 10030sin2100T（KN）（拉） （2）（1-1）截面内力：Q、N、M： 5030sinTQ（KN） 6.8630cosTN（KN）（压） 2550.030sinTM（KN-M） 1-6 一重物 P＝10 kN由均质杆 AB及绳索 CD支持如图示，杆的自重不计。求绳索CD的拉力及 AB杆在截面1-1上的内力． 解：（1）绳索CD拉力T： 0AM 4s i n 3 03s i n 3 0PT 1 3 . 3 3TK N （2）1-1 截面内力： 1 0c o s 3 01 3 . 3 3c o s 3 02 0 . 2NK N 1 3 . 3 3s i n 3 01 0s i n 3 01 . 6 6 7QK N   2 . 5s i n 3 01 . 5s i n 3 02 . 5 0MPTK Nm   1-7 杆AC及BD铰接于A、B、D三处如图示．在C端作用一铅直载荷P...