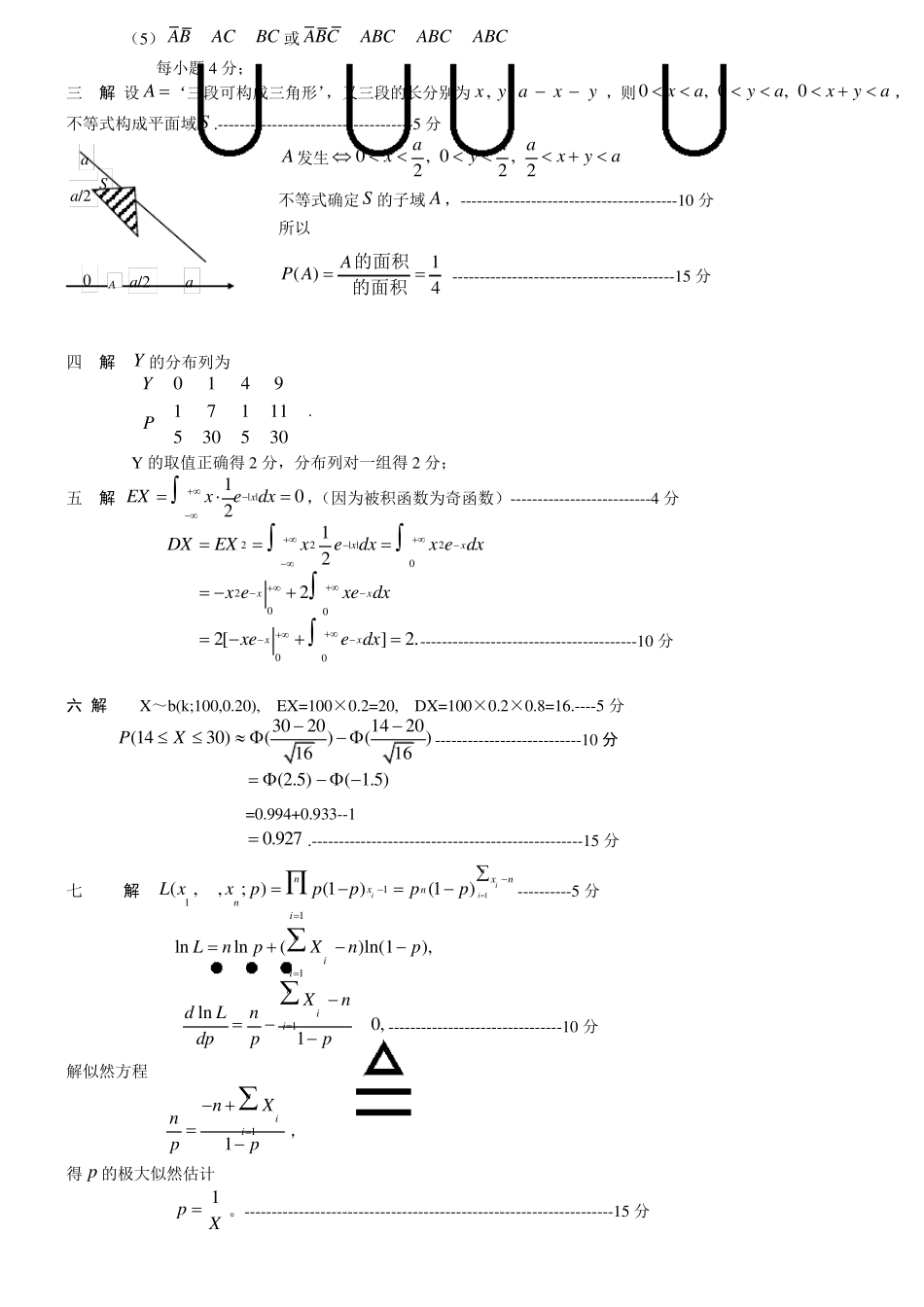
《概率论与数理统计》试题(1) 一 、 判断题(本题共15 分,每小题3 分。正确打“√”,错误打“×”) ⑴ 对任意事件 A 和 B,必有 P(AB)=P(A)P(B) ( ) ⑵ 设 A、B 是Ω中的随机事件,则(A∪B)-B=A ( ) ⑶ 若 X 服从参数为λ的普哇松分布,则 EX=DX ( ) ⑷ 假设检验基本思想的依据是小概率事件原理 ( ) ⑸ 样本方差2nS= n121)(XXnii 是母体方差 DX 的无偏估计 ( ) 二 、(20 分)设 A、B、C 是Ω中的随机事件,将下列事件用 A、B、C 表示出来 (1)仅 A 发生,B、C 都不发生; (2), ,A B C 中至少有两个发生; (3), ,A B C 中不多于两个发生; (4), ,A B C 中恰有两个发生; (5), ,A B C 中至多有一个发生。 三、(15 分) 把长为a 的棒任意折成三段,求它们可以构成三角形的概率. 四、(10 分) 已知离散型随机变量 X 的分布列为 210131111115651530XP 求2YX的分布列. 五、(10 分)设随机变量 X 具有密度函数| |1( )2xf xe , < x< , 求 X 的数学期望和方差. 六、(15 分)某保险公司多年的资料表明,在索赔户中,被盗索赔户占20%,以 X 表示在随机抽查100 个索赔户中因被盗而向保险公司索赔的户数,求(1430)PX. x 0 0.5 1 1.5 2 2.5 3 Ф(x) 0.500 0.691 0.841 0.933 0.977 0.994 0.999 七、(15 分)设12,,,nXXX 是来自几何分布 1()(1),1,2,,01kP Xkppkp, 的样本,试求未知参数 p 的极大 似 然 估计. 《概率论与数理统计》试题(1)评分标准 一 ⑴ ×;⑵ ×;⑶ √;⑷ √;⑸ ×。 二 解 (1) ABC (2) ABACBC 或 ABCABCABCABC ; (3) ABC 或 ABCABCABCABCABCABCABC ; (4) ABCABCABC ; (5)ABACBC 或ABCABCABCABC 每小题4 分; 三 解 设A ‘三段可构成三角形’,又三段的长分别为,,x y axy,则0, 0, 0xayaxya,不等式构成平面域S .------------------------------------5 分 A 发生0, 0,222aaaxyxya 不等式确定S 的子域A ,----------------------------------------10 分 所以 1( )4AP A 的面积S的面积 -----------------------------------------15 分 四 解 Y 的分布列为 014917111530530YP . Y 的取值正确得2 分,分布列对...