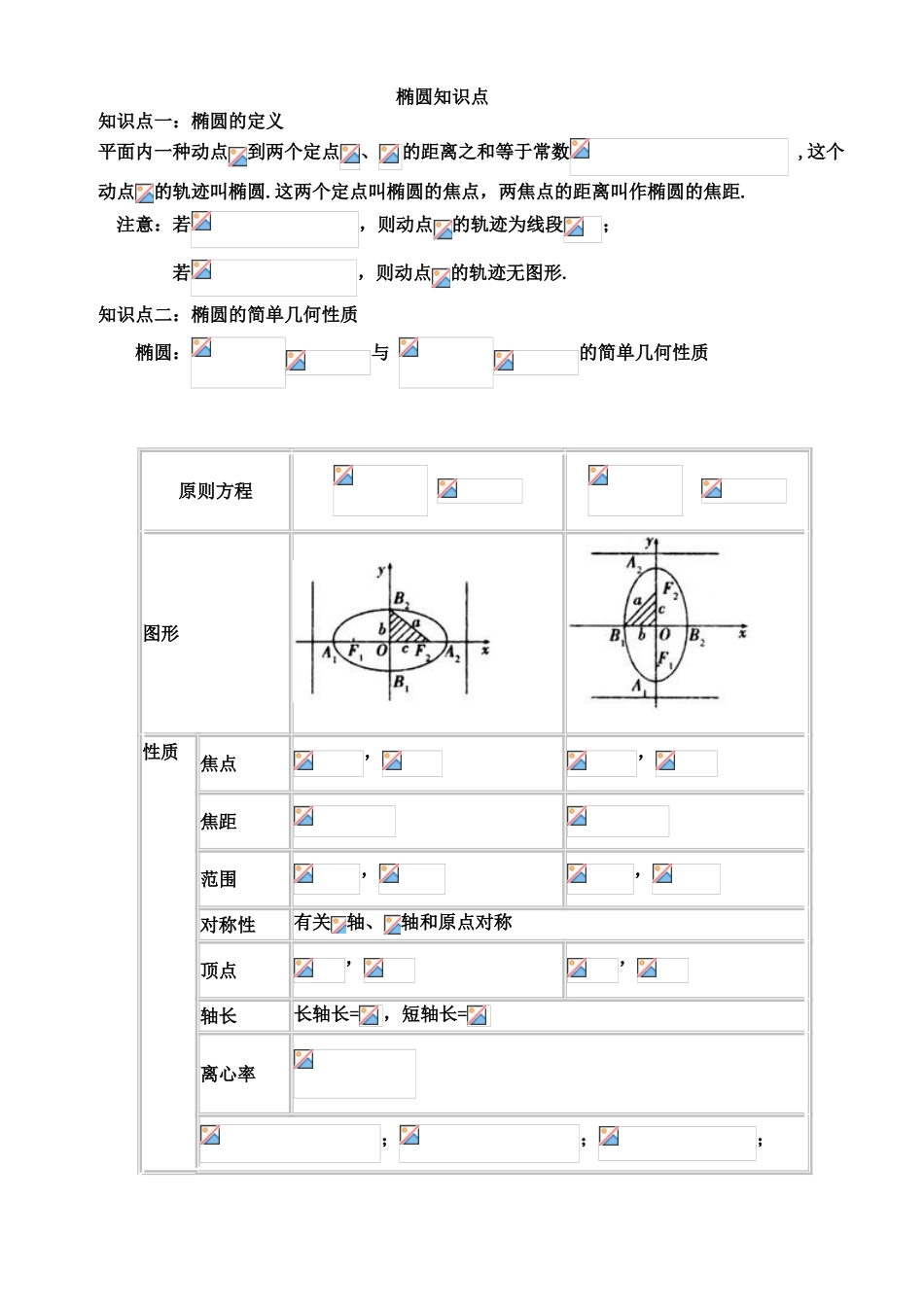
椭圆知识点知识点一:椭圆的定义平面内一种动点到两个定点、的距离之和等于常数 ,这个动点的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距. 注意:若,则动点的轨迹为线段; 若,则动点的轨迹无图形.知识点二:椭圆的简单几何性质 椭圆:与 的简单几何性质原则方程 图形性质焦点,,焦距 范围,,对称性有关轴、轴和原点对称顶点,,轴长长轴长=,短轴长= 离心率;;;(p 是椭圆上一点)1 . 椭 圆 原 则 方 程 中 的 三 个 量的 几 何 意 义 (3)找关系,根据已知条件,建立有关 a,b,c 或 m,n 的方程组.(4)解方程组,代入所设方程即为所求. 6.点与椭圆的位置关系:<1,点在椭圆内,=1,点在椭圆上,>1, 点在椭圆外。7.直线与椭圆的位置关系设直线方程 y=kx+m,若直线与椭圆方程联立,消去 y 得有关 x 的一元二次方程:ax2+bx+c=0(a≠0).(1)Δ>0,直线与椭圆有两个公共点;(2)Δ=0,直线与椭圆有一种公共点;(3)Δ<0,直线与椭圆无公共点. 8.弦长公式:若直线与圆锥曲线相交与、两点,则弦长 9.点差法:就是在求解圆锥曲线题目中,交代直线与圆锥曲线相交所截的线段中点坐标的时候,运用直线和圆锥曲线的两个交点,并把交点代入圆锥曲线的方程,并作差。求出直线的斜率,然后运用中点求出直线方程。环节:① 设直线和圆锥曲线交点为 , ,其中点坐标为 ,则得到关系式 , ..② 把 , 分别代入圆锥曲线的解析式,并作差,运用平方差公式对成果进行因式分解.其成果为③ 运用 求出直线斜率,代入点斜式得直线方程为 .