电子科大2010年信号与系统期末考题及标准答案

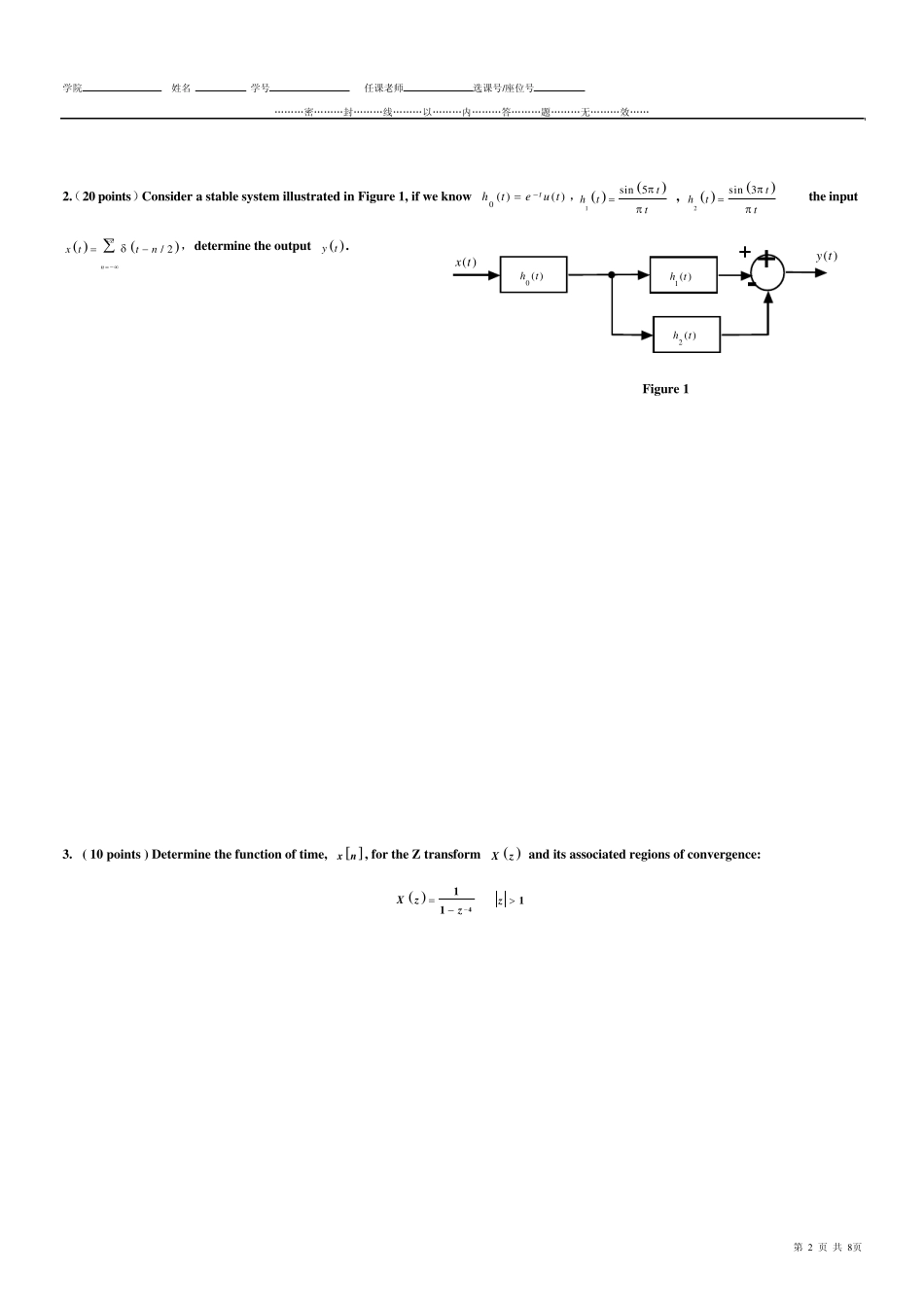
学院 姓名 学号 任课老师 选课号/座位号 ………密………封………线………以………内………答………题………无………效…… 第 1 页 共 8页 电子科技大学二零 一 零 至二零 一 一 学年第 一 学期期 末 考试 SIGNALS AND SYSTEMS 课程考试题 A 大纲 A 卷 （ 120 分钟） 考试形式： 一页纸开卷 考试日期 20 年 月 日 课程成绩构成：平时 10 分， 期中 20 分， 实验 10 分， 期末 60 分 一 二 三 四 五 六 七 八 九 十 合计 复核人签名 得分 签名 Attention: You must answer the following questions in English. 1.（15 points） Suppose  1xt and  2xt are two band-limited signals, where 200,0)(1forjX,500,0)(2forjX. Impulse-train sampling is performed on  1234/ 22ytxtxt to obtain   pnytynTtnT .Give out the expression of )( jYin terms of )(1jXand )(2jX，where )( jY is the Fourier transform of )(ty. Specify the largest values of the sampling period T which ensures that  ty is recoverable from  ty p. 学院 姓名 学号 任课老师 选课号/座位号 ………密………封………线………以………内………答………题………无………效…… 第 2 页 共 8页 2.（20 points）Consider a stable system illustrated in Figure 1, if we know )()(0tuetht，  1sin 5thtt ,  2sin 3thtt and the input  / 2 nx ttn，determine the output  y t . Figure 1 3. ( 10 points ) Determine the function of time,  x n , for the Z transform  Xz and its associated regions of convergence:  411Xzz 1z  )(0 th)(tx)(ty)(1 th)(2 th++- 学院 姓名 学号 任课老师 选课号/座位号 ………密………封………线………以………内………答………题………无………效…… 第 3 页 共 8页 4.（15 points）Consider a system illustrated in Figure 2(a). The input signal has the Fourier tansform ...