相似三角形的特殊模型一线三等角

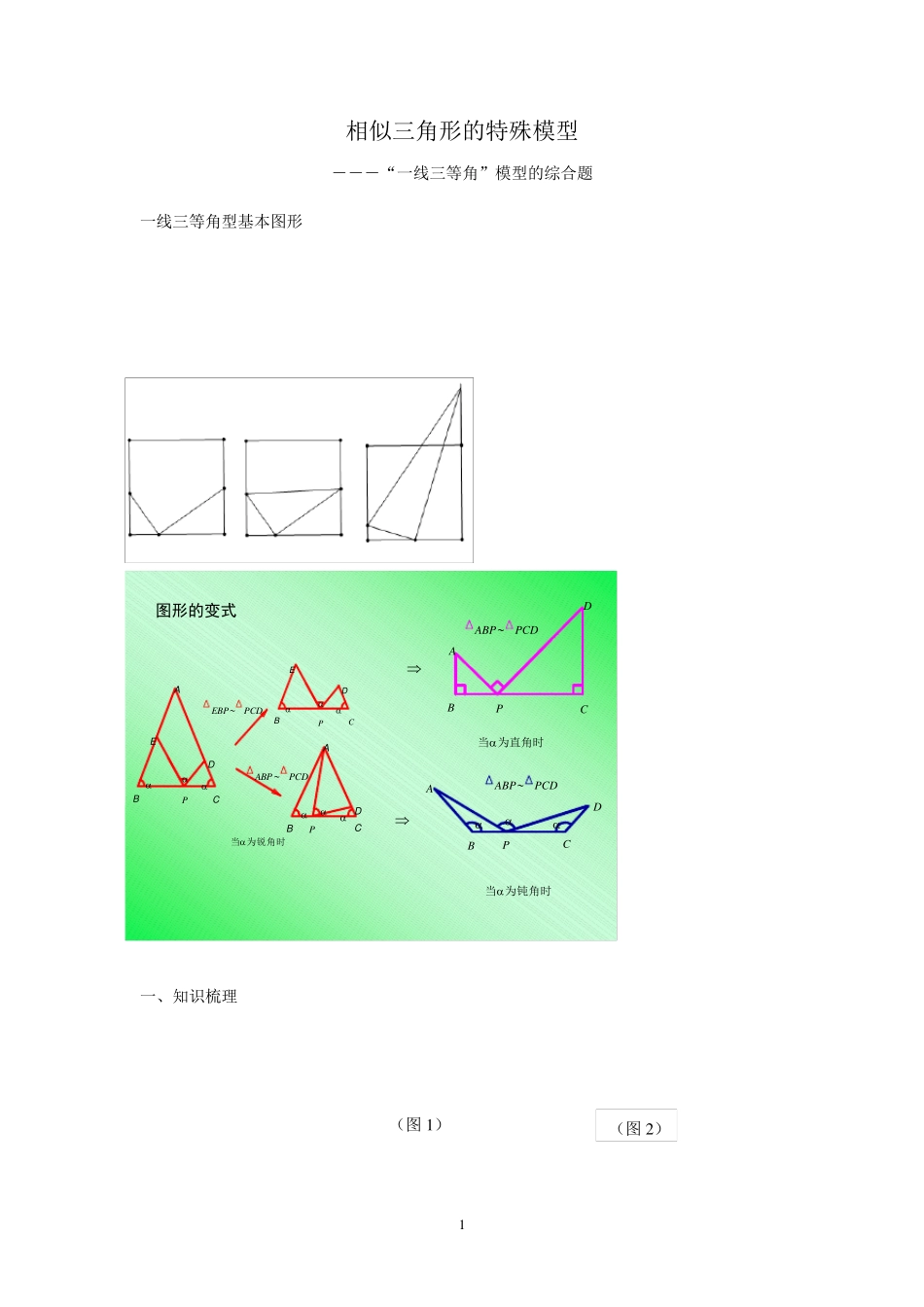
1 相似三角形的特殊模型 ―――“一线三等角”模型的综合题 一线三等角型基本图形 一、知识梳理 （图 1 ） （图 2 ） 图形的变式ABPCD当为直角时ABPPCDCBADP当为钝角时ABPPCDBACDE当为锐角时EBPPCDPBDECPBACDABPPCDP 2 （1）如图1：已知三角形ABC 中，AB=AC,∠ADE=∠B,那么一定存在的相似三角形有 ； （2）如图2：已知三角形ABC 中，AB=AC,∠DEF=∠B,那么一定存在的相似三角形有 ； (3) 如图2，若 AB＝AC，∠ B＝∠EDF, BD=CD, 连接DF ，那么一定存在的相似三角形有 . 二、例题解析 例1.如图，在边长为2 的等边三角形ABC 中，D 是BC 边上任意一点，AB 边上有一点E，AC边上有一点F，使∠EDF=∠ABC. 已知BD=1，BE= 31,求CF 的长. 练习 1.已知△ABC 中AB=AC=6、BC=8，∠BAC=120 度，D 是BC 边上任意一点，AB 边上有一点E，AC 边上有一点F，使∠EDF=∠C. 已知BD=6、BE=4 . 求:CF 的长 2.如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF=60°. （1）求证：△BDE∽△CFD ； （2）当 BD= 23，FC=1 时，求BE . 3 例2.在ABC中，OBCACC,3,4,9 0o是AB 上的一点，且52ABAO，点P 是AC上的一个动点，OPPQ 交线段BC 于点Q，（不与点B,C 重合），已知AP=2，求CQ . 练习 在直角三角形ABC 中，DBCABC,,9 0o是AB 边上的一点，E 是在AC 边上的一个动点，（与A,C 不重合），DFDEDF,与射线BC 相交于点F. (1)当点D 是边AB 的中点时，求证：DFDE ； (2)当 mDBAD ，求DFDE的值. 例3.已知在等腰三角形ABC 中，AB=AC,D 是BC 的中点，∠EDF=∠B. 求证：△BDE∽△DFE. 4 练习 在边长为4 的等边ABC中，D 是BC 的中点，点E、F 分别在AB、AC 上（点D 不与点C 、点B 重合），且保持ABCEDF,连接EF. (1)已知BE=1,DF=2.求DE 的值； (2)求∠BED=∠DEF. 例 4. 如图，已知边长为3 的等边三角形 ABC，点F 在边BC 上，CF=1，点E 是射线 BA 上一动点，以线段 EF 为边向右侧作等边三角形 EFG，直线 EG 与FG 分别交直线 AC 于点M、N， （1）写出图中与BEF相似的三角形； （2）证明其中一对三角形相似； （3）设 BE=x,MN=y，求y 与x 之间的函数关系式，并写出自变量 x 的取值范围. 练习 如图，在△ABC 中，8ACAB，1 0BC，D 是BC 边上的一个动点，点E 在AC...