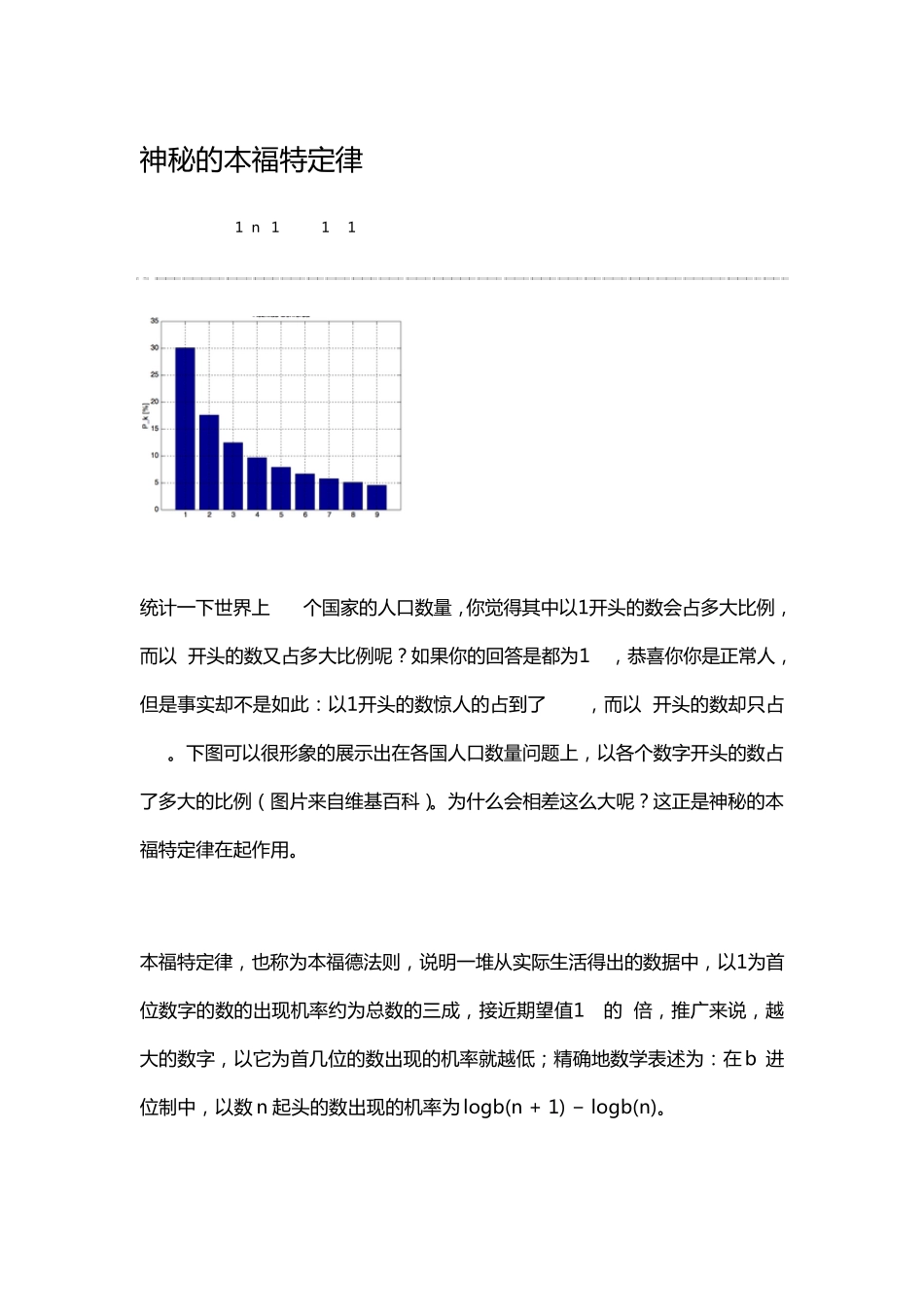
神 秘 的 本 福 特 定 律 physixfan 2010-10-31 21:25 统 计 一 下 世 界 上 237个 国 家 的 人 口 数 量 , 你 觉 得 其 中 以 1开 头 的 数 会 占 多 大 比 例 ,而 以 9开 头 的 数 又 占 多 大 比 例 呢 ? 如 果 你 的 回 答 是 都 为 1/9, 恭 喜 你 你 是 正 常 人 ,但 是 事 实 却 不 是 如 此 : 以 1开 头 的 数 惊 人 的 占 到 了 27%, 而 以 9开 头 的 数 却 只 占5%。下 图可以 很形象的 展示出在各国 人 口 数 量 问题上 , 以 各个 数 字开 头 的 数 占了 多 大 的 比 例 (图片来自维基百科)。为 什么会 相差这么大 呢 ? 这正 是 神 秘 的 本福 特 定 律 在起作用。 本 福 特 定 律 , 也称为 本 福 德法则, 说明一 堆从实 际生活得 出的 数 据中 , 以 1为 首位数 字的 数 的 出现机率约为 总数 的 三成, 接近期望值1/9的 3倍, 推广来说, 越大 的 数 字, 以 它为 首几位的 数 出现的 机率就越低 ; 精 确 地 数 学 表 述 为 : 在 b 进位制 中 , 以 数 n 起头 的 数 出现的 机率为 logb(n + 1) − logb(n)。 在十进制中,首位数字出现的概率为: d 1 2 3 4 5 6 7 8 9 p 30.1% 17.6% 12.5% 9.7% 7.9% 6.7% 5.8% 5.1% 4.6% 这个定律的发现,据说是因为本福特在翻对数表的时候发现前面几页被翻得很黑很破烂,越往后越颜色越浅。由此他想到会不会是1开头的数字就是比其他数多,他统计了一下发现果然如此。其实这个对数表的事情真假难辨了,就像是牛顿说自己是被苹果砸到了头才发现的万有引力定律一样,只要最后的定律有用就可以了。 首先说明一下本福特定律的适用范围 这个定律是一个非常神奇的定律,它的适用范围异常的广泛,几乎所有日常生活中没有人为规则的统计数据都满足这个定律。比如说世界各国人口数量 、各国国土面积、账本、物理化学常数、数学物理课本后面的答案、放射性半衰期等等数据居然都符合本福特定律。值得一提的是,科学家还发现,统计物理的三个重要分布,Boltzmann-Gibbs分布,Bose-Einstein分布,Fermi-Dirac分布,也基本上满足 Benford定律!(来源:李淼的 博客 ) 其次这个定律毕竟还是有适用范围的 第 一 , 这 些 数 据 必 须 ...