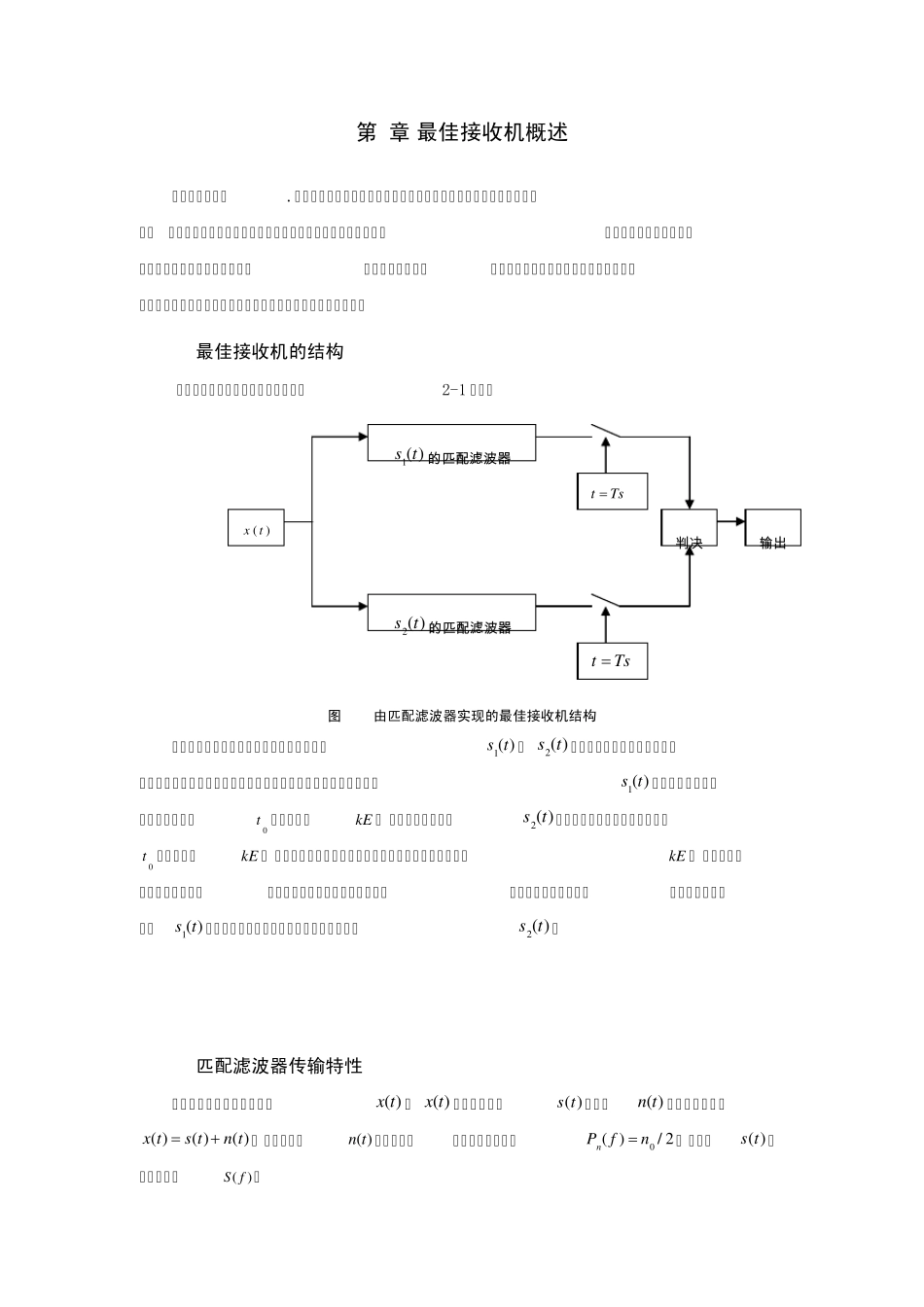
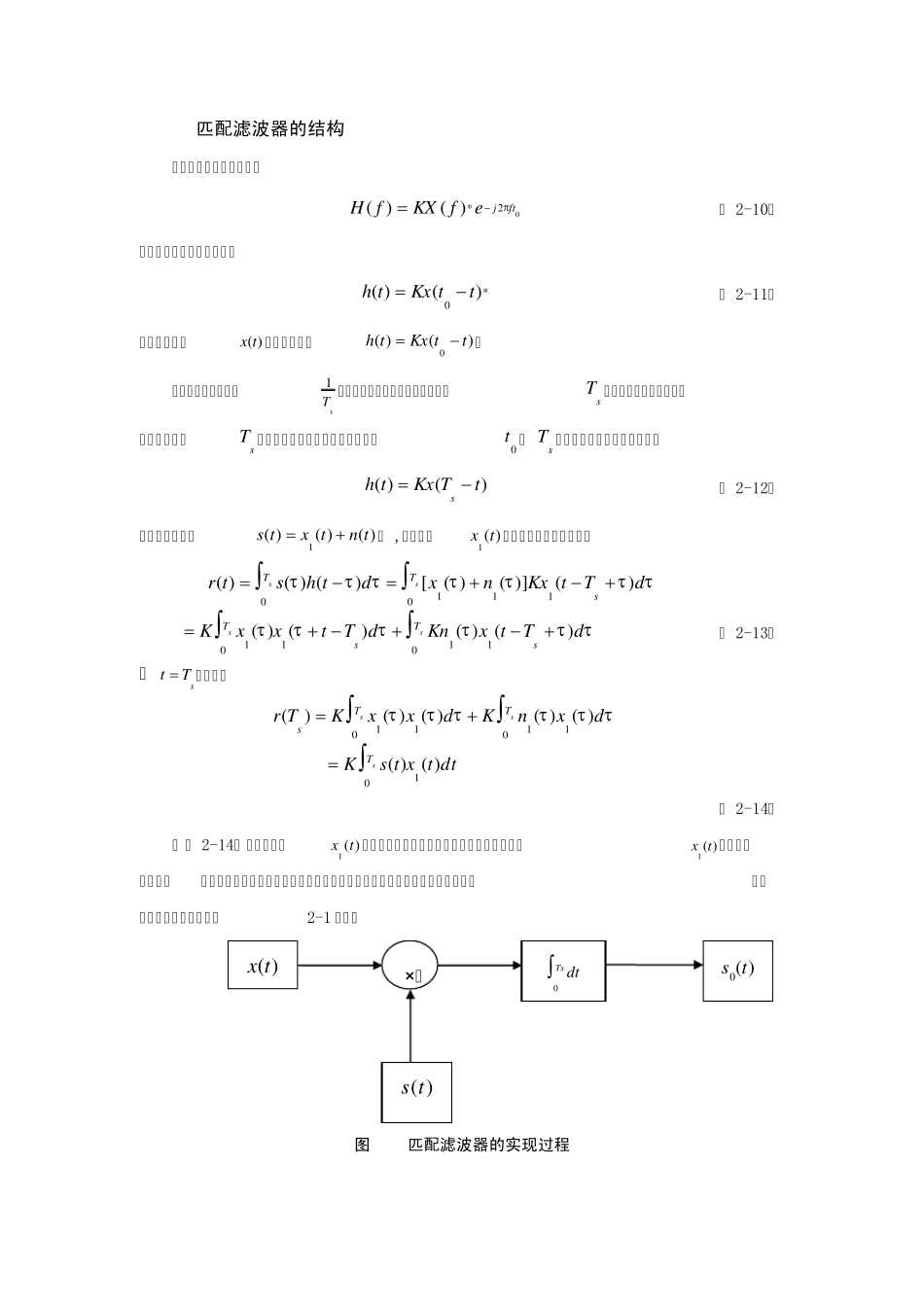
第2章 最佳接收机概述 接收机有很多种.“最佳”是个相对概念,不同条件、不同要求下的最佳接收机是不同的。 如白噪声信道的最佳接收机在瑞利衰落信道中就不是最佳的。本章讨论高斯白噪声信道中二元数字信号的最佳接收机。在高斯白噪声下,用匹配滤波器构成的接收机能得到最小的误码率。本章主要介绍匹配滤波器的原理和最佳接收机的结构。 2.1 最佳接收机的结构 二元数字信号的最佳接收机框图如图2-1 所示。 图2-1 由匹配滤波器实现的最佳接收机结构 发送段在任意一个码元间隔内发送两个波形1( )s t 、2( )s t 中的一个,接收机上、下两个支路的匹配滤波器分别对这两个波形匹配,所以当发送段发送波形1( )s t 时,上支路匹配滤波器在取样时刻0t 输出最大值kE , 当发送端发送波形2( )s t 时下支路匹配滤波器在取样时刻0t 输出最大值kE , 而与接收信号不匹配的滤波器在取样时刻输出的值小于kE 。 所以判决器的任务是根据上、下两支路取样值的大小进行判决,如上支路取样值打大,认为接收到的信号为1( )s t ;如下支路取样值大,认为接收到的信号为2( )s t 。 2.2 匹配滤波器传输特性 设匹配滤波器的输入信号为( )x t ,( )x t 是由接收信号( )s t 和噪声( )n t 两部分构成,即( )( )( )x ts tn t, 在表达式中( )n t 是白噪声,双边功率谱密度为0( )/ 2nPfn, 而信号( )s t 的频谱函数为( )S f 。 1( )s t 的 匹 配 滤 波 器 2( )s t 的 匹 配 滤 波 器 判 决 ( )xttTs tTs 输出 根据线性叠加原理,匹配滤波器的输出 也由信号( )os t 和噪声( )on t 两部分构成,即 0( )( )( )oy ts tn t ( 2-1) 设( )os t 的频谱为 ,根据信号与系统理论得 ( )( )( )oSfS f H f ( 2-2) 求( )S f 的傅里叶反变换,可得到输出信号( )os t 为 2( )( )( )iftos tS f H f edf ( 2-3) 输出噪声0t 的功率谱密度为 20|)(|2)(fHNfPon ( 2-4) 匹配滤波器在0t 时刻的输出信号值为 2( )( )( )iftos tS f H f edf ( 2-5) 则在0t 时刻输出信号的瞬时功率为200|)(|ts,输出噪声平均功率为 2( )2OnNPH fdf ( 2-6) 所以0t 时刻输出的信噪比为 22202( )( )( )( )2ojftooOnX f H f edfs trNPH fdf...