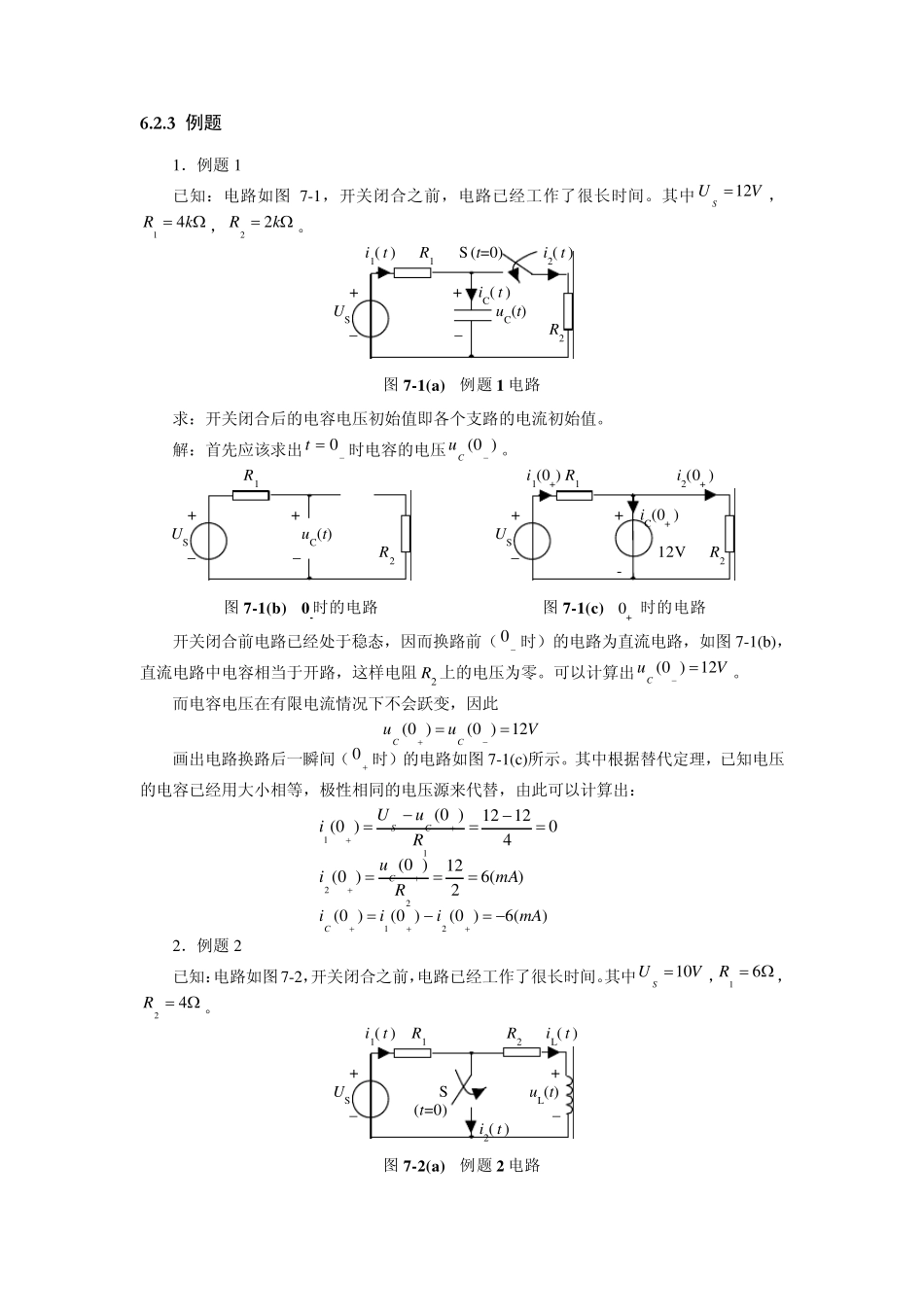
第六章 一阶电路 重点: 1 . 电路微分方程的建立 2 . 三要素法 3 . 阶跃响应 难点: 1 . 冲激函数与冲激响应的求取 2 . 有跃变时的动态电路分析 含有动态元件(电容或电感等储能元件)的电路称为动态电路。回忆储能元件的伏安关系为导数(积分)关系,因此根据克希霍夫定律列写出的电路方程为微积分方程。所谓“一阶”、“二阶”电路是指电路方程为一阶或二阶微分方程的电路。 本章只讨论一阶电路,其中涉及一些基本概念,为进一步学习第十五章打下基础。 6.1 求解动态电路的方法 6.1.1 求解动态电路的基本步骤 在介绍本章其他具体内容之前,我们首先给出求解动态电路的基本步骤。 1.分析电路情况,得出待求电量的初始值; 2.根据克希霍夫定律列写电路方程; 3.解微分方程,得出待求量。 由上述步骤可见,无论电路的阶数如何,初始值的求取、电路方程的列写和微分方程的求解是解决动态电路的关键。 6.2.1 一阶微分方程的求解 一、一阶微分方程的解的分析 初始条件为)()0()()(tfttf的非齐次线性微分方程 BwAxdtdx 的解)(tx由两部分组成:)()()(txtxtxph。其中)(txh为原方程对应的齐次方程的通解,)(txp为非齐次方程的一个特解。 二、)(txh的求解 由齐次方程的特征方程,求出特征根p,直接写出齐次方程的解pthKetx)(,根据初始值解得其中的待定系数K,即可得出其通解。 三、)(txp的求解 根据输入函数的形式假定特解的形式,不同的输入函数特解形式如下表。 由这些形式的特解代入原微分方程使用待定系数法,确定出方程中的常数Q 等。 四、一阶微分方程的解的求取 )()()()(txKetxtxtxpptph 将初始条件00 )(Xtx代入该式: 000)()(0XtxKetxppt 由此可以确定常数K,从而得出非齐次方程的解。 6.2 电路的初始条件 从以上有关的高等数学知识的复习我们知道,求解微分方程时,n 阶常系数线性微分方程的通解中含有n 个待定的积分常数,它们需要由微分方程的初始条件来确定。而描述动态电路的初始条件,是指方程中输出变量的初始值及其1~n 阶导数的初始值(对于一阶电路,仅指输出变量的初始值)。 6.2.1 几个概念 1.换路(Switching)——在电路分析中,我们把电路与电源的接通、切断,电路参数的突然改变,电路联接方式的突然改变等等,统称为换路。 2.过渡过程——电路在换路时将可能改变原来的工作状态,而这种转变需要一个过程,工程上称为...