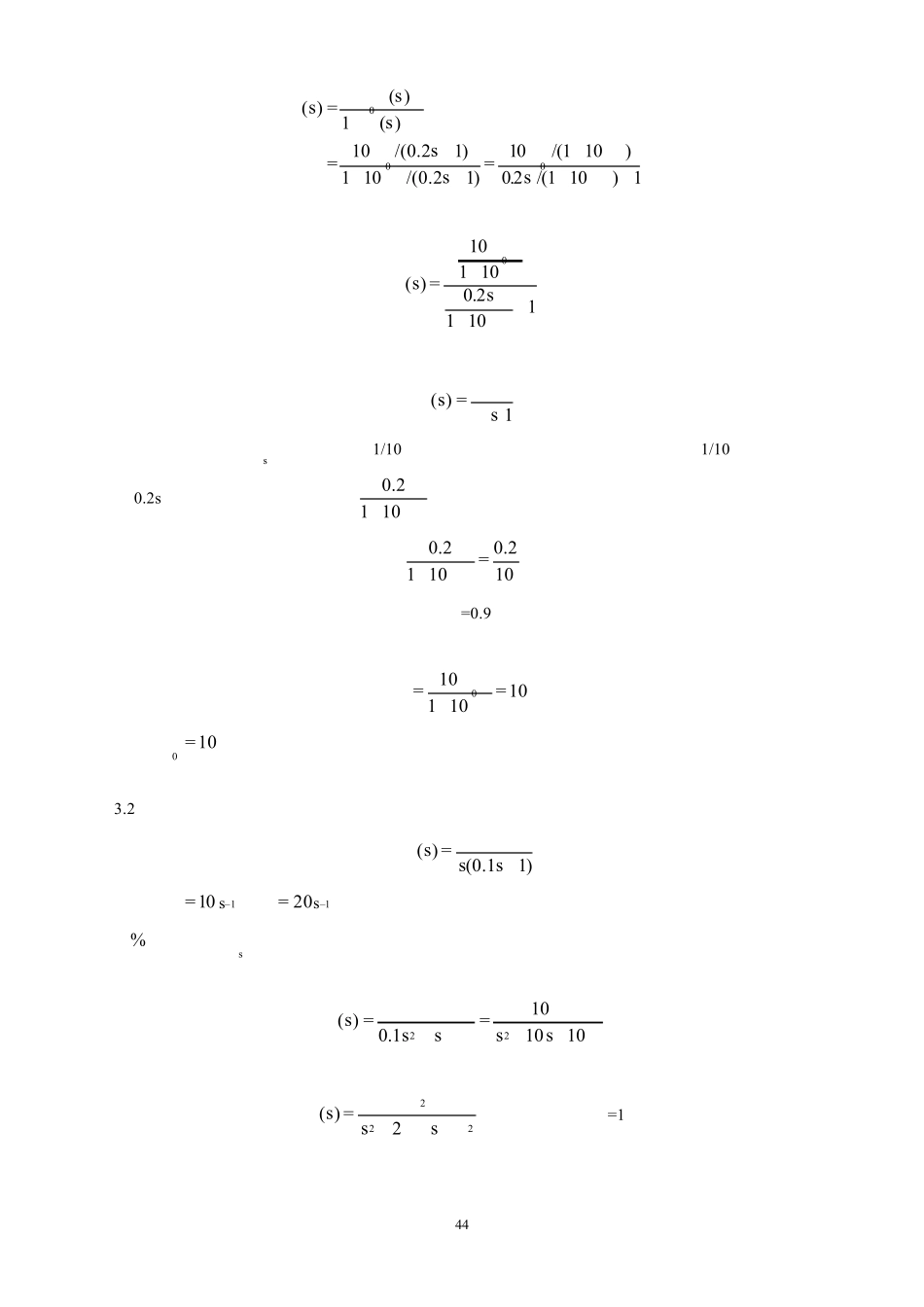
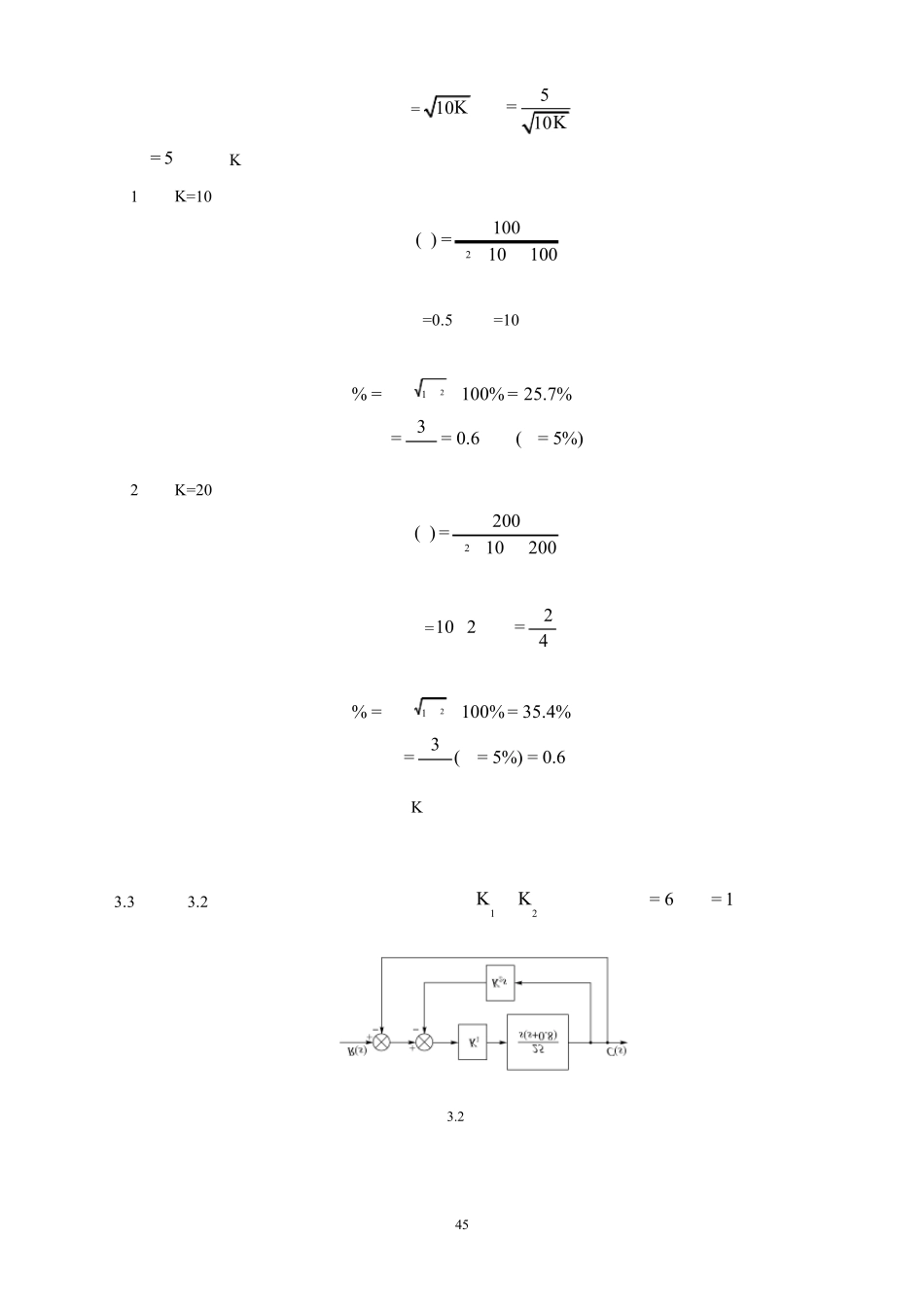
43第 3 章控制系统的时域分析法本章介绍了根据系统的时间响应去分析系统的稳定性、动态性能和稳态误差的有关问题。其主要内容有:(1)自动控制系统的时域分析法,根据控制系统在典型输入信号的作用下输出响应的时域数学表达式和响应曲线,直接分析系统等系统的稳定性、动态性能和稳态误差的品质。时域分析法具有直观、准确的优点。(2)稳定性是系统能否正常工作的首要条件。系统的稳定性取决于系统自身的结构和参数,与外作用的大小和形式无关。线性系统稳定的充要条件是其特征方程的根均位于左半 s平面(即系统的特征根全部具有负实部)。劳斯稳定判据是从系统的闭环特征方程,间接判定系统的稳定性的。(3)对于稳定的控制系统,工程上常用单位阶跃响应的最大超调量σ%,调节时间 ts和稳态误差等性能指标,评价系统性能的优劣。典型的一阶、二阶系统的性能指标与系统的参数有严格的对应关系,必须牢固掌握。对一阶、二阶系统分析的结果,往往是分析高阶系统的基础。当高阶系统具有一对闭环主导极点时(通常是一对共轭复数极点),可以用一个二阶系统近似,并以此估算高阶系统的动态性能。(4)系统的稳态误差不是系统自身的固有特性,它与系统的结构参数及输入信号的形式都有关。系统的型别ν决定了系统对典型输入信号的跟踪能力。提高系统的型别和增大开环放大系数可以减小或消除系统的稳态误差。但这和稳定性有矛盾。在要求高的场合可用复合控制。教材习题同步解析3.1系统结构图如图 3.1 所示。已知传递函数12.010)(+=ssG,现采用加负反馈的方法,将调节时间st减小为原来的1/10,并保证总放大倍数不变。试确定参数hK 和0K 的数值。解:加负反馈后,系统闭环传递函数为:图 3.1系统结构图44000( )( )1( )10/(0.21)10/(1 10)1 10/(0.21)0.2 /(1 10) 1hhhhKGssGs KKsKKKssKΦ=+++==++++化为标准的时间常数表达式0101 10( )0.211 10hhKKssK+Φ=++而典型的一阶系统传递函数为( )1KsTsΦ=+因此,欲将调节时间st减小为原来的 1/10,则反馈系统的时间常数 T应该为原来的 1/10。原系统的时间常数为 0.2s,而反馈系统的时间常数为0.21 10hK+,故有0.20.21 1010hK =+hK =0.9由于保证总放大倍数不变,则有010101 10hKKK==+所以100 =K。3.2某单位负反馈系统的开环传递函数为( )(0.11)KKG sss=+试分别求出10K=s– 1 和20=Ks–1 时,系统的阻尼比ξ和无阻尼自然振荡角频率nω ,及单位阶跃响应的超调量%σ和调节时间s...