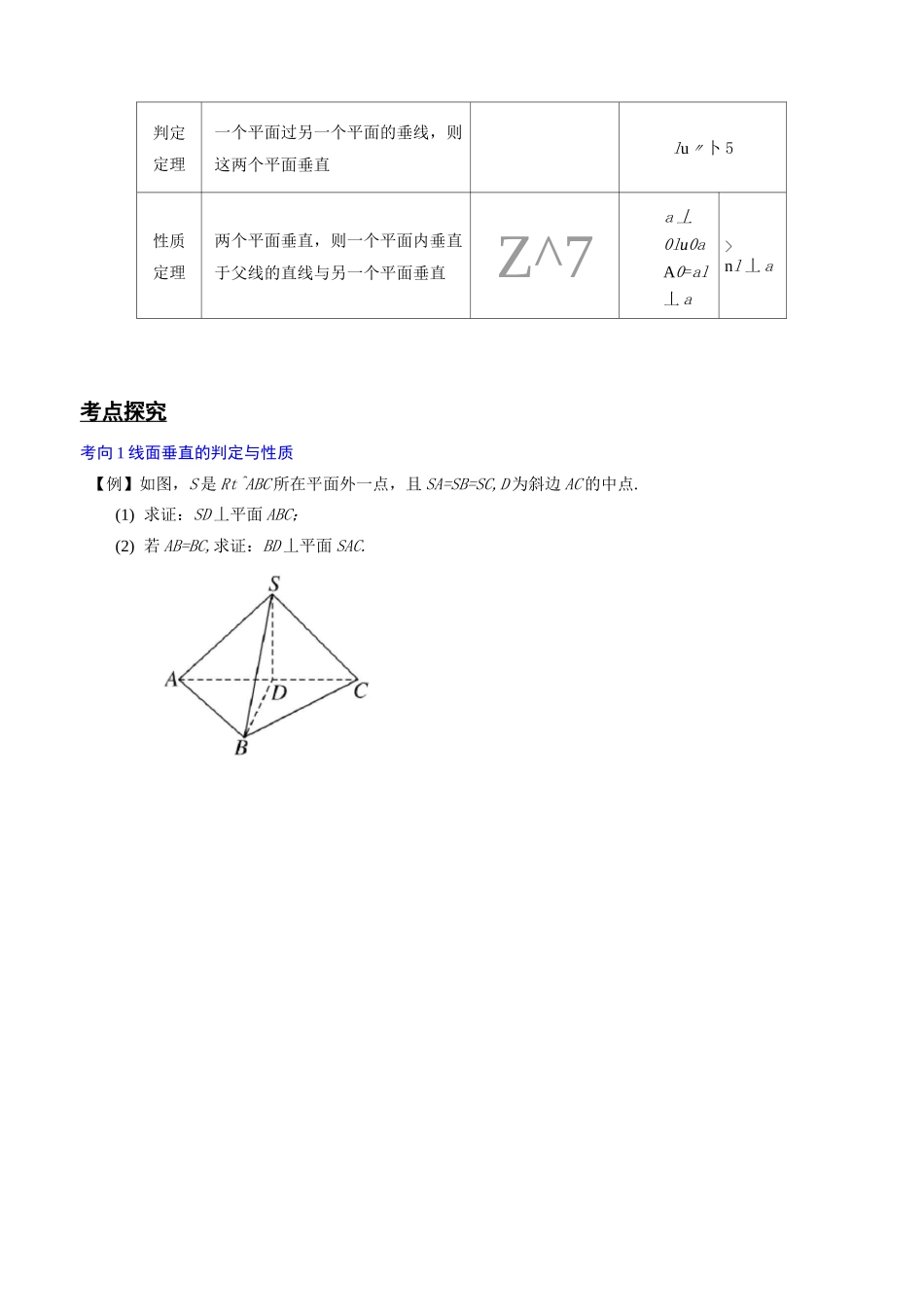
专题 50 直线与平面、平面与平面的垂直专题知识梳理 1.直线与平面垂直(1)定义如果直线 l 与平面«内的任意一条直线都垂直,则直线 l 与平面«互相垂直,记作 l 丄«,直线 l 叫做平面«的垂线,平面«叫做直线 l 的垂面.(2)判定定理与性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直1a,bDaaAb=Ol 丄 al丄 b 丿>□l 丄 a性质定理垂直于同一个平面的两条直线平行a\卜a 丄 a]'□a〃bb 丄 aj2. 直线和平面所成的角(1)定义平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.若一条直线垂直于平面,它们所成的角是直角,若一条直线和平面平行,或在平面内,它们所成的角是 0°的角.(2)范围:2]3. 平面与平面垂直(1) 二面角的有关概念① 二面角:从一条直线出发的两个半平面所组成的图形叫做二面角;② 二面角的平面角:在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.(2) 平面和平面垂直的定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(3) 平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面垂直lu〃卜 5性质定理两个平面垂直,则一个平面内垂直于父线的直线与另一个平面垂直Z^7a 丄0lu0aA0=al丄 a>nl 丄 a考点探究 考向 1 线面垂直的判定与性质【例】如图,S 是 Rt^ABC 所在平面外一点,且 SA=SB=SC,D 为斜边 AC 的中点.(1) 求证:SD 丄平面 ABC;(2) 若 AB=BC,求证:BD 丄平面 SAC.题组训练1.如图,已知丹丄平面 ABC,BC 丄 AC,则图中直角三角形的个数为2.如图,在四棱锥 P—ABCD 中,PA 丄底面 ABCD,AB 丄 AD,AC 丄 CD,ZABC=60°,PA=AB=BC,E 是 PC 的中点.证明:(1) CD 丄 AE;(2) PD 丄平面 ABE.3•设 m,n 是两条不同的直线,a,“是两个不同的平面:① 若 m 丄 n,nila,贝 Vm 丄 a;② 若 m〃“,B 丄 a,贝 9m 丄 a;③ 若 m 丄〃,n 丄〃,n 丄 a,贝 Vm 丄 a;④ 若 m 丄 n,n 丄〃,〃丄 a,贝 Vm 丄 a.上述命题中为真命题的是(填序号).考向 2 面面垂直的判定与性质【例】如图,在四棱锥 PABCD 中,AB〃CD,AB 丄 AD,CD=2AB,平面 PAD 丄平面 ABCD,PA 丄 AD,点...