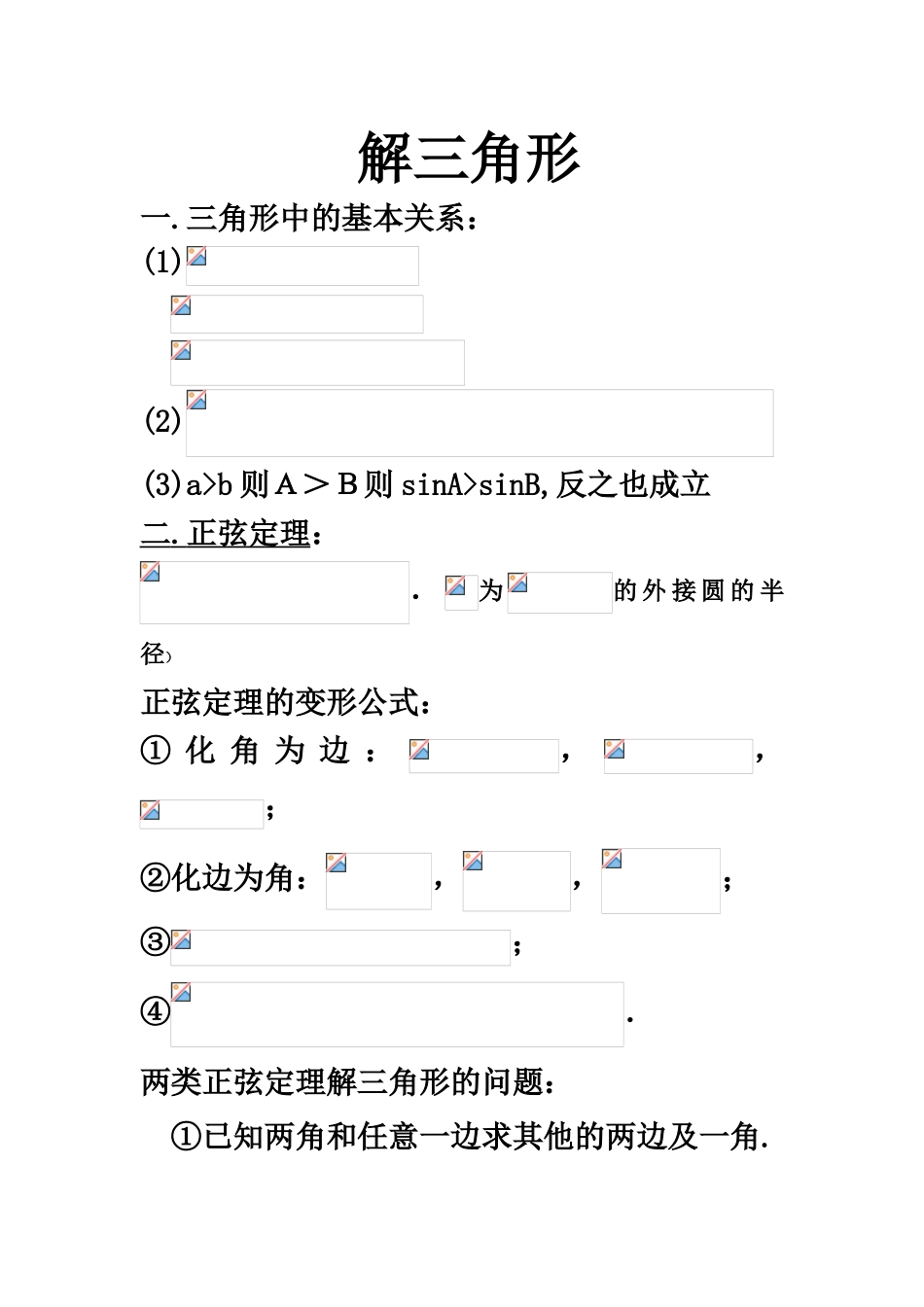
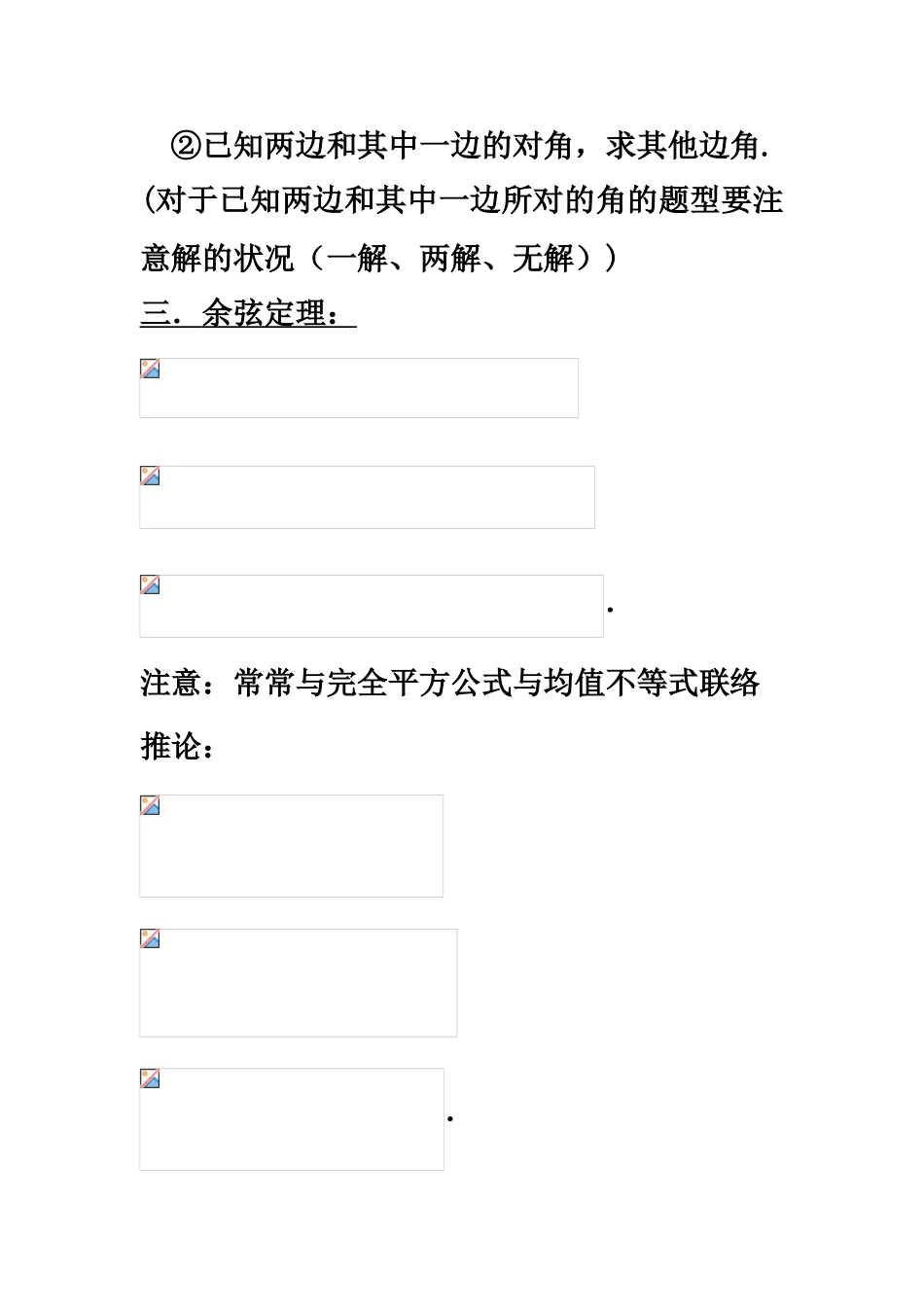
解三角形一.三角形中的基本关系:(1) (2)(3)a>b 则A>B则 sinA>sinB,反之也成立二 . 正弦定理 :.为的 外 接 圆 的 半径)正弦定理的变形公式:① 化 角 为 边 :,,;②化边为角:,,;③;④.两类正弦定理解三角形的问题:①已知两角和任意一边求其他的两边及一角.②已知两边和其中一边的对角,求其他边角.(对于已知两边和其中一边所对的角的题型要注意解的状况(一解、两解、无解))三. 余弦定理: .注意:常常与完全平方公式与均值不等式联络推论:.①若,则;②若,则;③若,则.余弦定理重要处理的问题:(1).已知两边和夹角求其他的量。(2).已知三边求其他的量。注意:解三角形与判定三角形形状时,实现边角转化,统一成边的形式或角的形式四、三角形面积公式: 等差数列一.定义:假如一种数列从第 2 项起,每一项与 它的前一项的差等于同一种常数,则这个数列称为等差数列,这个常数称为等差数列的公差.二.符号表达:(n>=1)三.判断数列是不是等差数列有如下四种措施:(1) ( 可 用 来 证明)(2)2()(可用来证明)(3)(为常数)(4)是一种有关 n 的 2 次式且无常数项四.等差中项,,成等差数列,则 称为 与 的等差中项.若,则称 为与的等差中项.五.通项公式: (是一种有关的一次式,一次项系数是公差)通项公式的推广:; .六.等差数列的前 项和的公式:①(注意运用性质尤其是下标为奇数)②(是一种有关 n 的 2 次式且无常数项,二次项系数是公差的二分之一)七.等差数列性质:(1)若则;(2)若则.(3) (4)(5)①若项数为,则, 且,.②若项数为,则,且,( 其 中,).( 6 ) 若 等 差 数 列 { an} {bn} 的 前 n 项 和 为 则八.等差数列前 n 项和的最值(1)运用二次函数的思想: (2)找到通项的正负分界线若 则 有最大值,当 n=k 时取到的最大值 k 满足若 则 有最大值,当 n=k 时取到的最大值 k 满足等比数列一.定义、假如一种数列从第 项起,每一项与它的前一项的比等于同一种常数,则这个数列称为等比数列,这个常数称为等比数列的公比.二.符号表达:注:①等比数列中不会出现值为 0 的项;② 奇数项同号,偶数项同号(3)合比性质的运用三.数列是不是等比数列有如下四种措施:①( 可 用 来 证明)②()(可用来证明)③(为非零常数).(指数式)④ 从前 n 项和的形式(只用来判断)四.等比中项:在与中间插入一种数,使 ,...