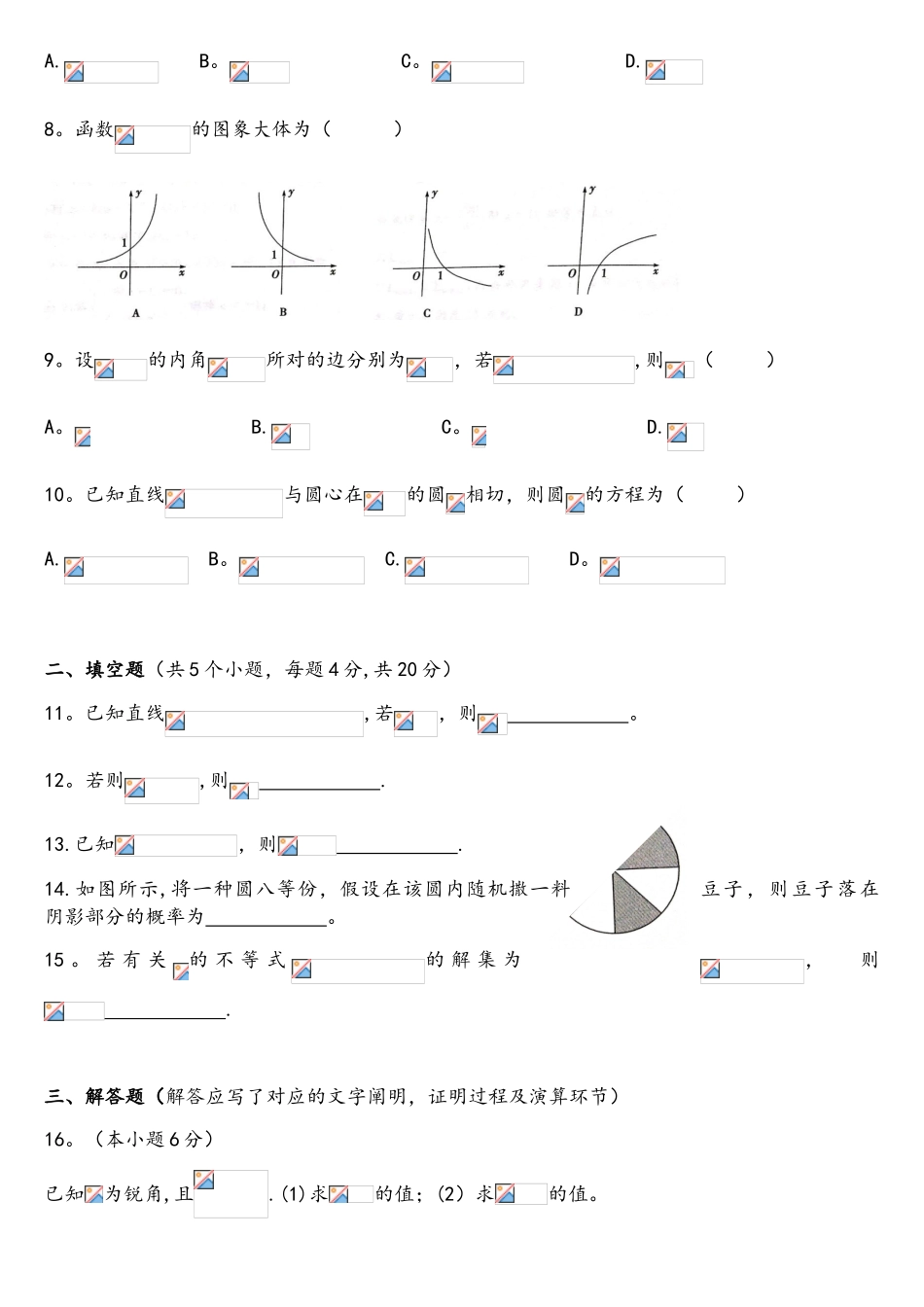
湖南省一般高中学业水平考试真题数 学一、选择题(共 10 个小题,每题 4 分,共 40 分)1。下列几何体中为圆锥的是( )2。已知集合,则( )A. B. C 。 D.3。函数的最小正周期是( )A. B. C。 D.4.执行如图所示的程序框图,若输入的值为 2,则输出的值为( )A. B. C。 D。5。某班有男生 30 人,发生 20 人,现用分层抽样的措施从中抽取 10 人参与一项活动,则抽取的男生的人数为( )A。 B。 C. D。6.已知向量,则( )A。 B. C。 D.7.已知,则下列不等式恒成立的是( )A. B。 C。 D.8。函数的图象大体为( )9。设的内角所对的边分别为,若,则( )A。 B. C。 D.10。已知直线与圆心在的圆相切,则圆的方程为( )A. B。 C. D。二、填空题(共 5 个小题,每题 4 分,共 20 分)11。已知直线,若,则 。12。若则,则 .13.已知,则 .14.如图所示,将一种圆八等份,假设在该圆内随机撒一料豆子,则豆子落在阴影部分的概率为 。15 。 若 有 关的 不 等 式的 解 集 为,则 .三、解答题(解答应写了对应的文字阐明,证明过程及演算环节)16。(本小题 6 分)已知为锐角,且.(1)求的值;(2)求的值。17.(本小题 8 分)甲乙两个学习小组各有 7 名同学,在某次数学测试中,测试成绩的茎叶图如图所示,(1)求甲组同学成绩的中位数和乙组同学成绩的众数;(2)从这次测试成绩在 90 分以上的学生中,随机抽取 1 名学生,求抽到的这名学生来自甲组的概率.甲乙8 97 66 5 08 2 2 36 29 1 3 518。如图所示,三棱柱中,底面,.(1)求证:平面;(2)已知,且异面直线与所成的角为,求三棱柱的体积。CABA1B1C119.(本小题 8 分)已知数列满足且。(1)求数列的通项公式;(2)已知数列满足,设,若数列为等比数列,求数列的前项和;20。(本小题 10 分)已知二次函数.(1)若为偶函数,求 的值;(2)判断函数在区间内与否有零点,请阐明理由;(3)已知函数存在最小值,求的最大值.