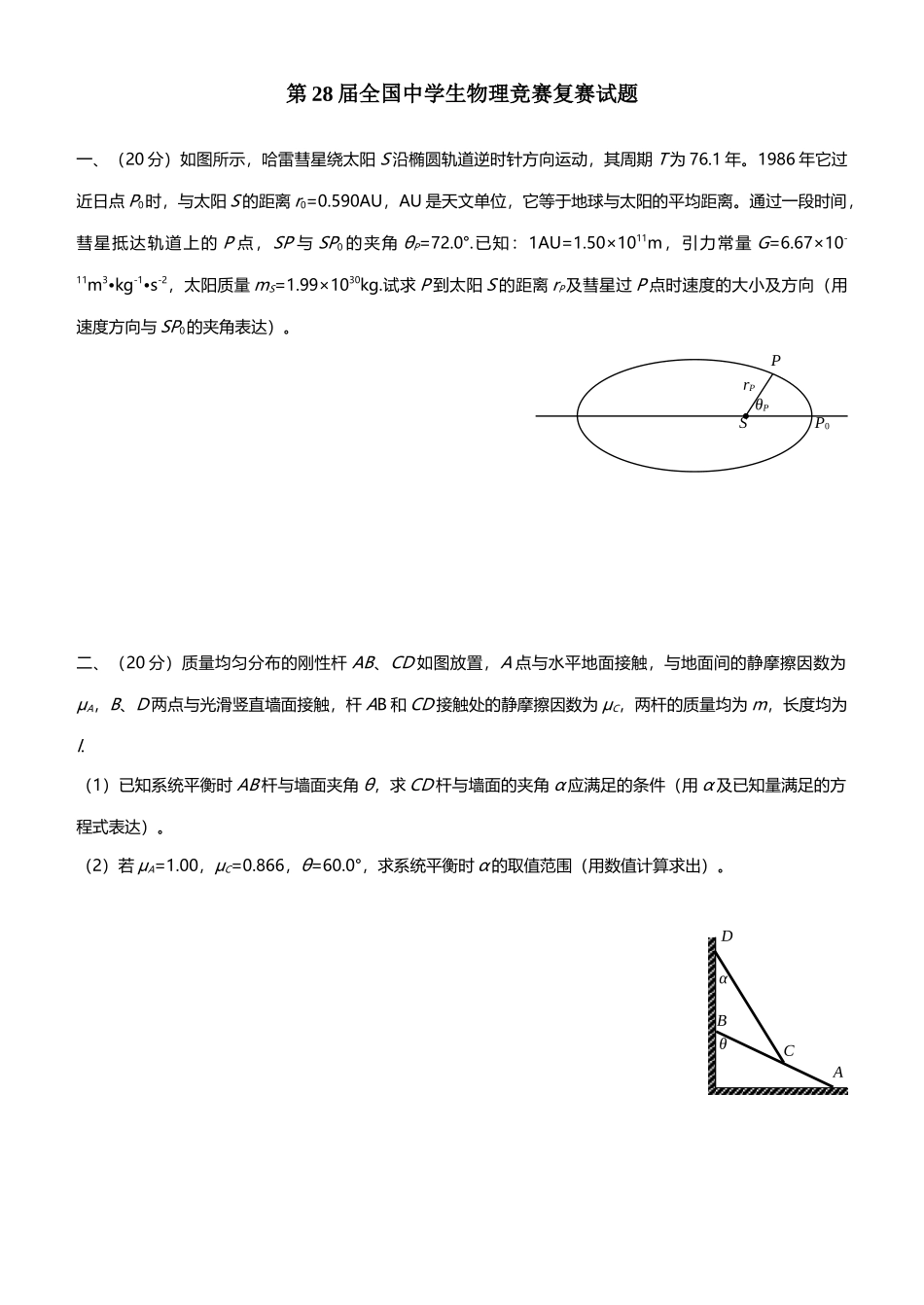
第 28 届全国中学生物理竞赛复赛试题一、(20 分)如图所示,哈雷彗星绕太阳 S 沿椭圆轨道逆时针方向运动,其周期 T 为 76.1 年。1986 年它过近日点 P0时,与太阳 S 的距离 r0=0.590AU,AU 是天文单位,它等于地球与太阳的平均距离。通过一段时间,彗星抵达轨道上的 P 点,SP 与 SP0 的夹角 θP=72.0°.已知:1AU=1.50×1011m,引力常量 G=6.67×10-11m3•kg-1•s-2,太阳质量 mS=1.99×1030kg.试求 P 到太阳 S 的距离 rP及彗星过 P 点时速度的大小及方向(用速度方向与 SP0的夹角表达)。二、(20 分)质量均匀分布的刚性杆 AB、CD 如图放置,A 点与水平地面接触,与地面间的静摩擦因数为μA,B、D 两点与光滑竖直墙面接触,杆 AB 和 CD 接触处的静摩擦因数为 μC,两杆的质量均为 m,长度均为l.(1)已知系统平衡时 AB 杆与墙面夹角 θ,求 CD 杆与墙面的夹角 α 应满足的条件(用 α 及已知量满足的方程式表达)。(2)若 μA=1.00,μC=0.866,θ=60.0°,求系统平衡时 α 的取值范围(用数值计算求出)。SP0PθPrPθαABCD三、(25 分)人造卫星绕星球运行的过程中,为了保持其对称轴稳定在规定指向,一种最简单的措施就是让卫星在其运行过程中同步绕自身的对称轴旋转。但有时为了变化卫星的指向,又规定减慢或者消除卫星的旋转。减慢或者消除卫星旋转的一种措施是所谓的“YO—YO”消旋法,其原理如图。设卫星是二分之一径为 R、质量为 M 的薄壁圆筒,其横截面如图所示。图中 O 是圆筒的对称轴。两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的 Q、Q'(位于圆筒直径两端)处,另一端各拴有一质量为 m/2 的小球。正常状况下,绳绕在圆筒外表面上,两小球用插销分别锁定在圆筒表面上的 P0、P0'处,与卫星形成一体,绕卫星的对称轴旋转。卫星自转的角速度为 ω0.若要使卫星减慢或停止旋转(消旋),可瞬间撤去插销释放小球,让小球从圆筒表面甩开,在甩开的整个过程中,从绳与圆筒表面相切点到小球的那段绳都是拉直的。当卫星转速逐渐减小到零时,立虽然绳与卫星脱离,接触小球与卫星的联络,于是卫星停止转动。已知此时绳与圆筒的相切点刚好在 Q、Q'处。试求:(1)当卫星角速度减至 ω 时绳拉直部分的长度 l;(2)绳的总长度 L;(3)卫星从 ω0到停转所经历的时间 t.QQ'm/2m/2P0P0'Oω0四、(20 分)空间某区域存在匀强电场和匀强磁场,...