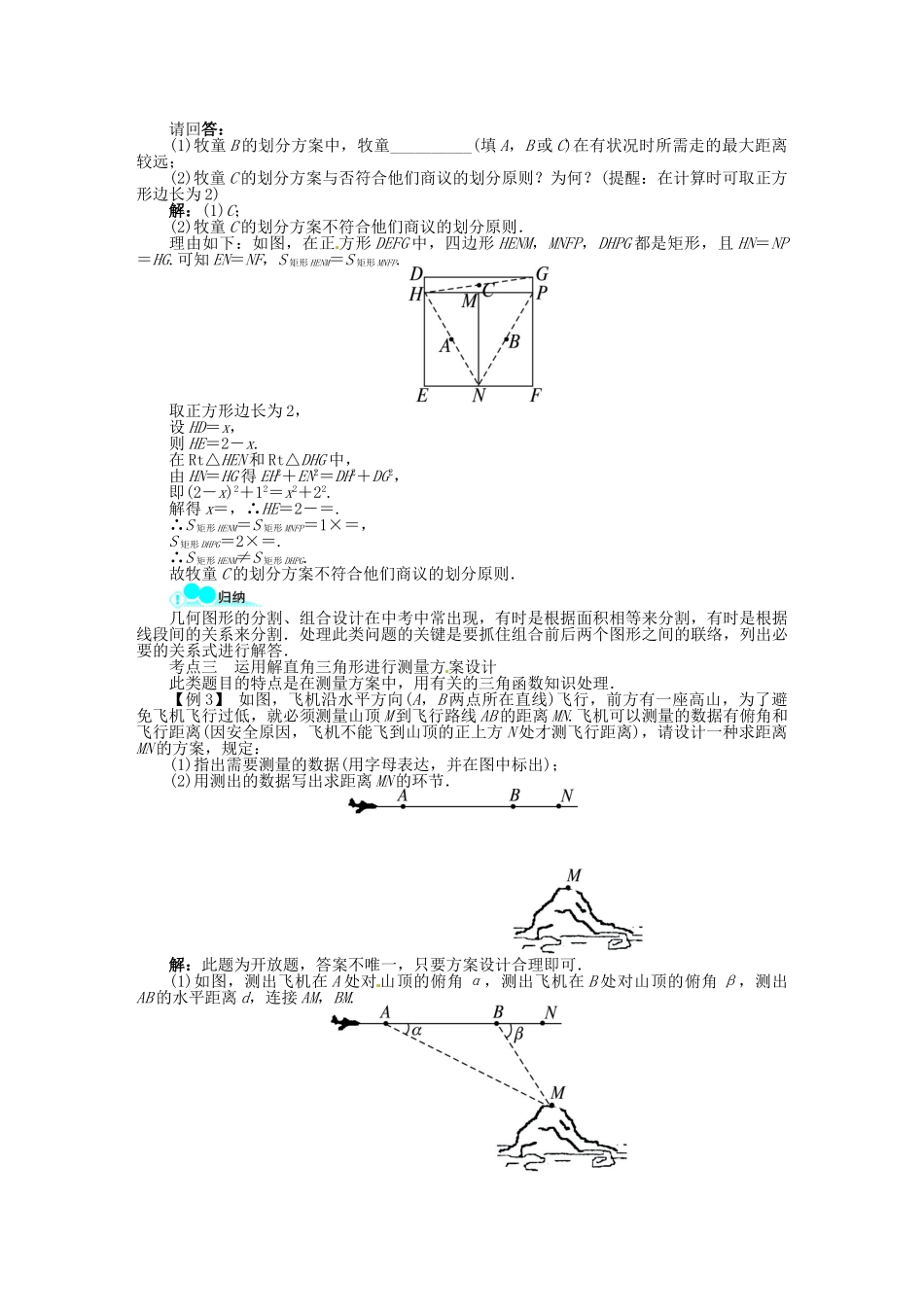
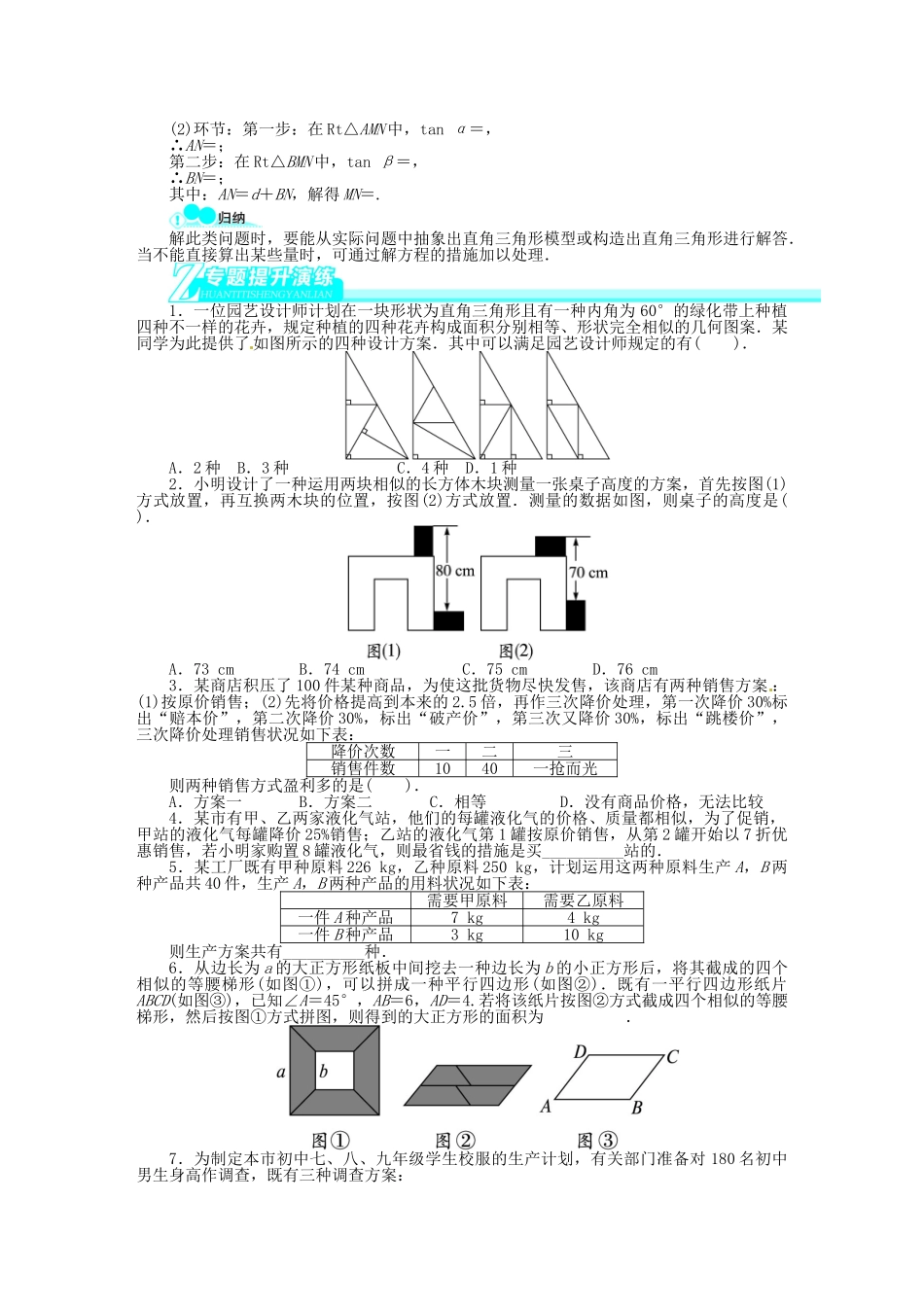
专题六 方案设计与决策方案设计题包括运用代数知识处理的方案讨论问题和图案设计型问题.此类问题常以生产、生活、市场经济等社会热点问题为素材,在各地中考中备受关注.这些问题新奇灵活,多以填空题、解答题形式出现.考点一 运用方程(或不等式)、一次函数等知识进行方案决策设计本类题是一类综合性较强的分析决策问题,涵盖了方程、不等式、一次函数等有关知识,考察学生的综合分析、归纳能力.【例 1】 2011 年 4 月 28 日,以“天人长安,创意自然——都市与自然友好共生”为主题的世界园艺博览会在西安隆重开园,这次园艺会的门票分为个人票和团体票两大类,其中个人票设置有三种:票的种类夜票(A)平日一般 票(B)指定日一般票(C)单价(元/张)60100150某小区居委会为奖励“友好家庭”,欲购置个人票 100 张,其中 B 种票的张数是 A 种票张数的 3 倍还多 8 张,设购置 A 种票张数为 x,C 种票张数为 y.(1)写出 y 与 x 之间的函数关系式;(2)设购票总费用为 w 元,求出 w(元)与 x(张)之间的函数关系式;(3)若每种票至少购置 1 张,其中购置 A 种票不少于 20 张,则有几种购票方案?并求出购票总费用至少时,购置 A,B,C 三种票的张数.解:(1)y=-4x+92.(2)w=60x+100(3x+8)+150(-4x+92)=-240x+14 600.(3)由题意,得解之,得 20≤x<23. x 是正整数,∴x 可取 20,21,22.∴共有 3 种购票方案. w=-240x+14 600,k=-240<0,∴w 伴随 x 的增大而减小,当 x=22 时,w 的取值最小.即当 A 票购置 22 张时,购票的总费用至少.∴购票总费用至少时,购置 A,B,C 三种票的张数分别为 22,74,4.本类型题目重要特点有:(1)当运用不等关系来确定取值范围时,要结合不等式的取值范围来讨论;(2)当运用方程来确定取值范围时,往往运用解的整数性来解答.以上两种类型都一般与一次函数相联络,在处理实际问题时,要注意其实际意义,确定自变量的取值范围是处理一次函数最值的关键.考点二 运用几何知识进行方案决策设计运用几何知识进行方案设计,不仅要有一定的几何作图能力,并且要能纯熟地运用几何的有关性质及全等、相似、图形变换、方程及三角函数的有关知识,并注意充足发挥分类讨论、类比归纳、猜想验证等数学思想措施的作用.【例 2】 三个牧童 A,B,C 在一块正方形的牧场上看守一群牛,为保证公平合理,他们商议将牧场划分为三块分别看守,划分的原则是:...