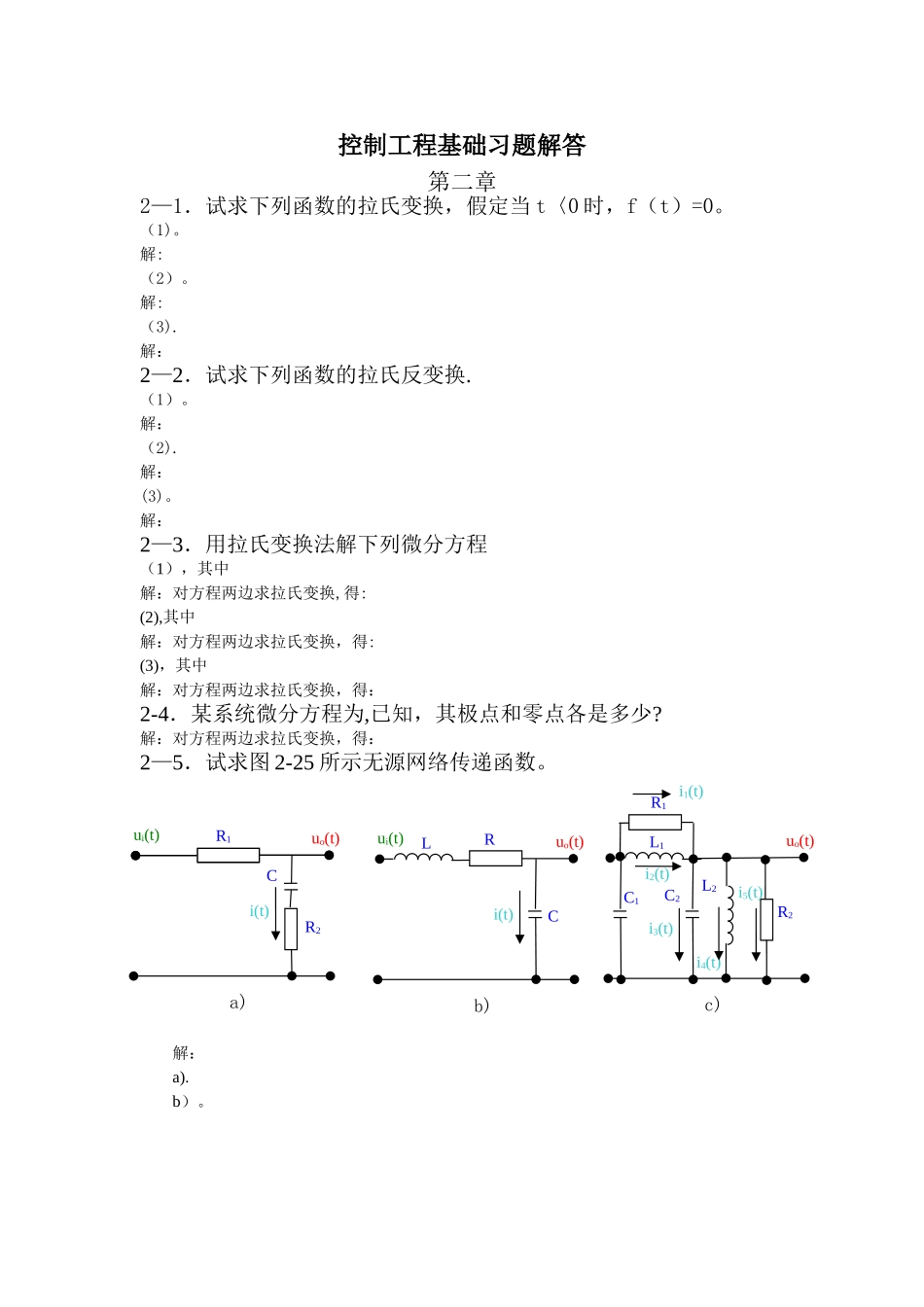
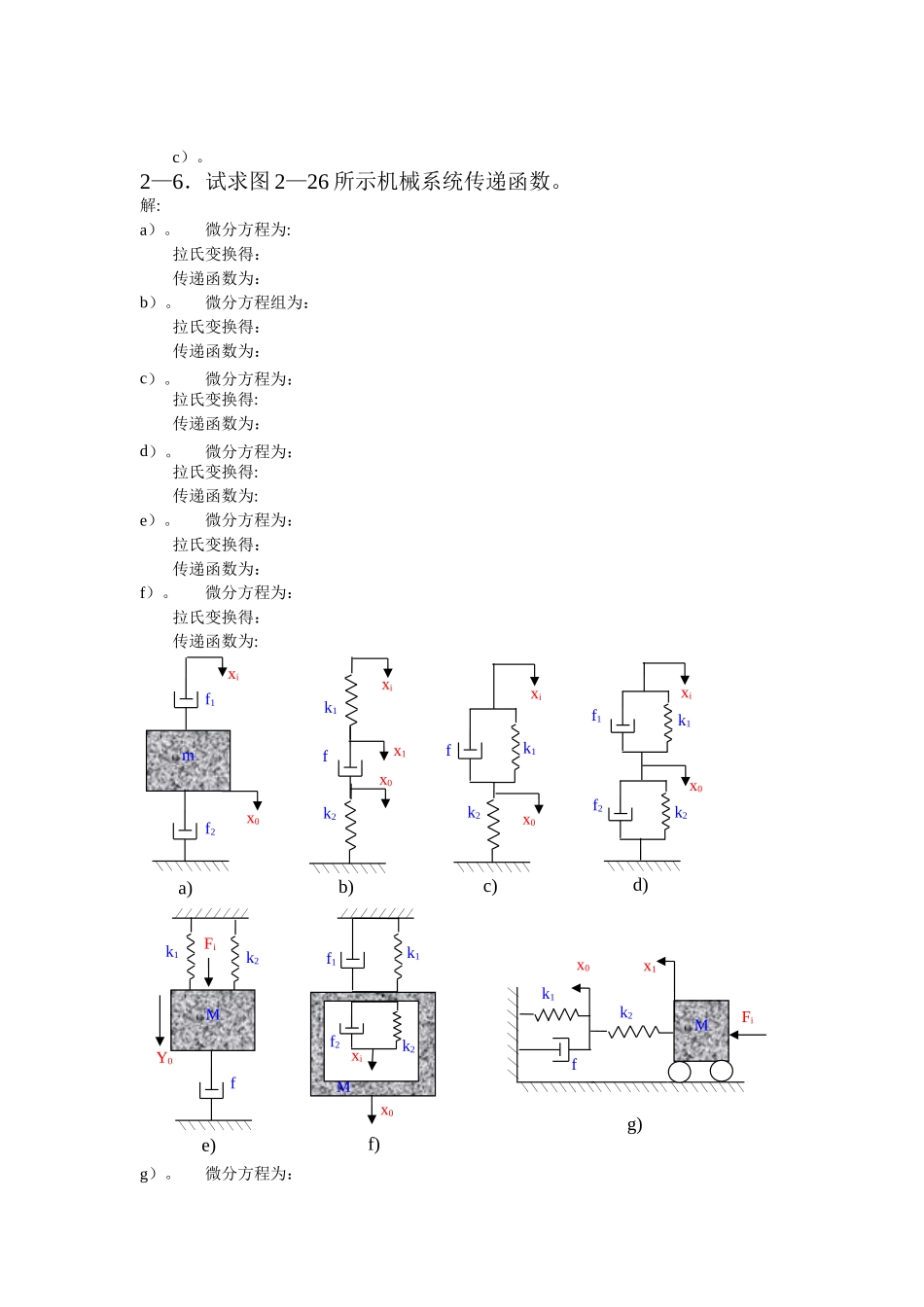
控制工程基础习题解答第二章2—1.试求下列函数的拉氏变换,假定当 t〈0 时,f(t)=0。(1)。解:(2)。解:(3).解:2—2.试求下列函数的拉氏反变换.(1)。解:(2).解:(3)。解:2—3.用拉氏变换法解下列微分方程(1),其中解:对方程两边求拉氏变换,得:(2),其中解:对方程两边求拉氏变换,得:(3),其中解:对方程两边求拉氏变换,得:2-4.某系统微分方程为,已知,其极点和零点各是多少?解:对方程两边求拉氏变换,得:2—5.试求图 2-25 所示无源网络传递函数。解:a). b)。 i(t)CR1R2ui(t)uo(t)a)ui(t)i(t)CRuo(t)b)Luo(t)c)i1(t)i2(t)R2L2C1L1R1C2i3(t)i4(t)i5(t)c)。2—6.试求图 2—26 所示机械系统传递函数。解:a)。微分方程为:拉氏变换得:传递函数为:b)。微分方程组为:拉氏变换得:传递函数为:c)。微分方程为:拉氏变换得:传递函数为:d)。微分方程为:拉氏变换得:传递函数为:e)。微分方程为:拉氏变换得:传递函数为:f)。微分方程为:拉氏变换得:传递函数为:g)。微分方程为:mf1mxix0ff2a)k1k2fb)xix0k1k2fc)xix0k1k2fe)x0k1k2Md)xix0k1f1f2MFiY0xik2f1f2MFik1k2x0f)g)x1x1拉氏变换得:传递函数为:2—7.对于如图 2-27 所示系统,试求从作用力 F1(t)到位移 x2(t)的传递函数.其中 B 为粘性阻尼系数。作用力 F2(t)到位移 x1(t)的传递函数又是什么?解:从作用力 F1(t)到位移 x2(t)微分方程为:拉氏变换得:传递函数为:从作用力 F2(t)到位移 x1(t)系统为对称系统所以传递函数为:2-8.证明 2—28a 与 b 表示的系统是相似系统( 即 证 明 两 个 系 统 的传 递 函 数 具 有 相 同 的形式)。解:a)。 用等效阻抗法做:拉氏变换得:传递函数为:b).用等效刚度法做:拉氏变换得:传递函数为:可见当:时,两系统的数学模型完全相同。2—9.如图 2—29 所示系统,试求(1)以 Xi(s)为输入,分别以 X0(s)、Y(s)、B(s)、E(s)为输出的传递函数。(2)以 N(s)为输入,分别以 X0(s)、Y(s)、B(s)、E(s)为输出的传递函数.解:(1)(2)2—10.试画出图 2—30 系统的框图,并求出其传递函数。其中 Fi(t)为输入力,X0(t)为输出位移。G1(s)E(s)+ -B(s)Xi(s)H(s)N(s)Y(s)+ +X0(s)G2(s)fk1k2F1x1(t)F2x2(t)m1m2i(t)C1R1R2ui(t)uo(t)a)k1k2f2b)xiC2f1x0解:框图不是唯一的,如可画成:2—11.化简图 2-31 所示各系统框图;并求其传递函数.f2Fi(t)k1k2x0(t)M2M1f2f1+ +Fi(s)X0(s)a)。 XiG1+ -H1+-X0G2+ -G3H3H2G1+ -XiH1++X0G2+ -G3H2+ -G4G1+ +XiH1+ -X0G2+ -G3H2G4-G1+ -XiH1+ +X0G2+ -H2H3b)。 XiG1+ -H1+-X0G2H2XiG1+ -H1X0XiX0G1+ -XiH1++X0G2+ -G3H2+ -G1+ -XiH1X0G2+ -H2+ -G1+ -XiX0+ -H2+ -+ -XiX0+ -c)。 d)。 XiX0+ -XiX0G1+ +Xi+ -X0+H2G4-G1+ +Xi+ -X0G4Xi+ -X0G4XiX0G1+ -XiH1+ +X0G2+ -H2H3+ -XiX0H3XiX0