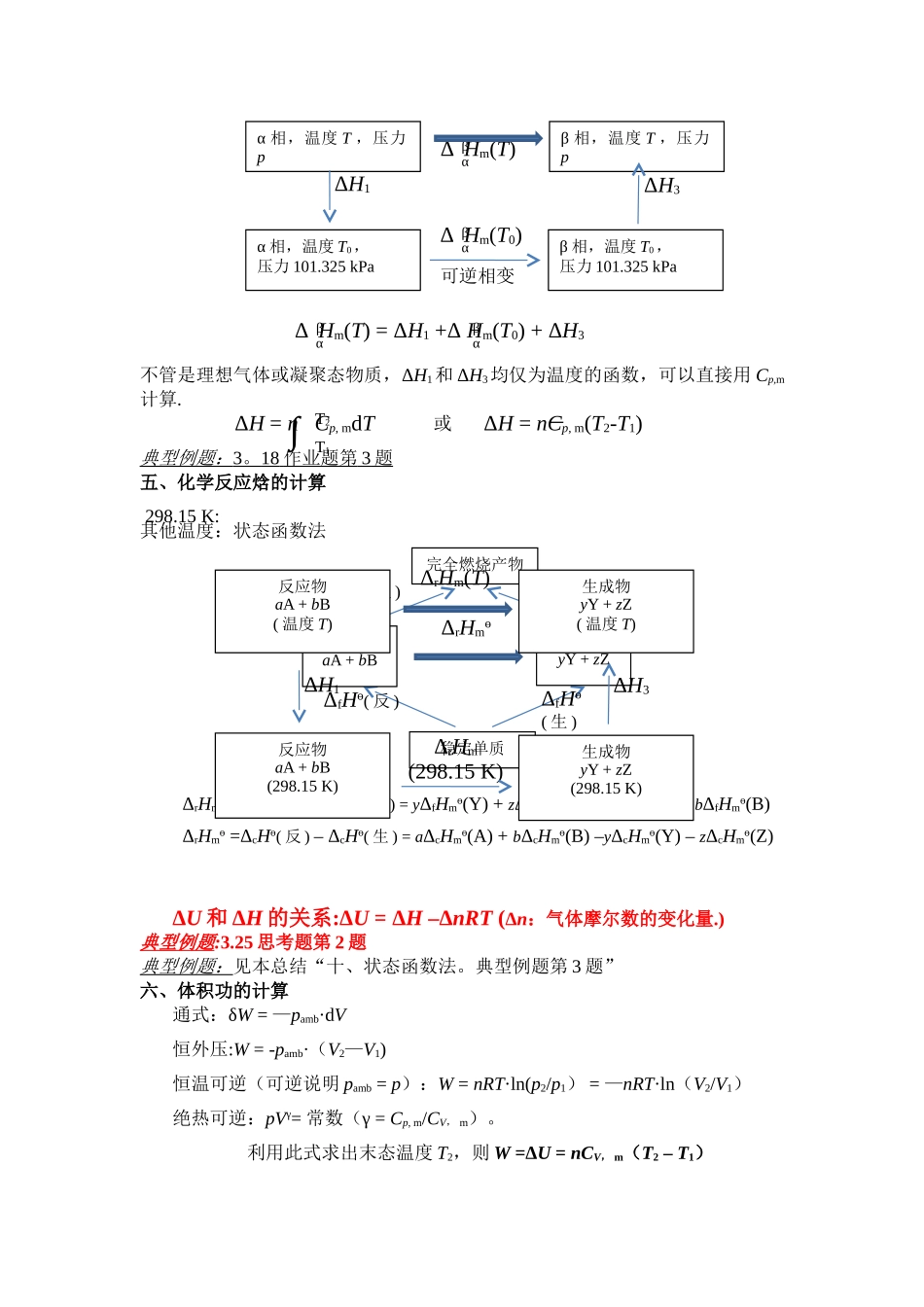
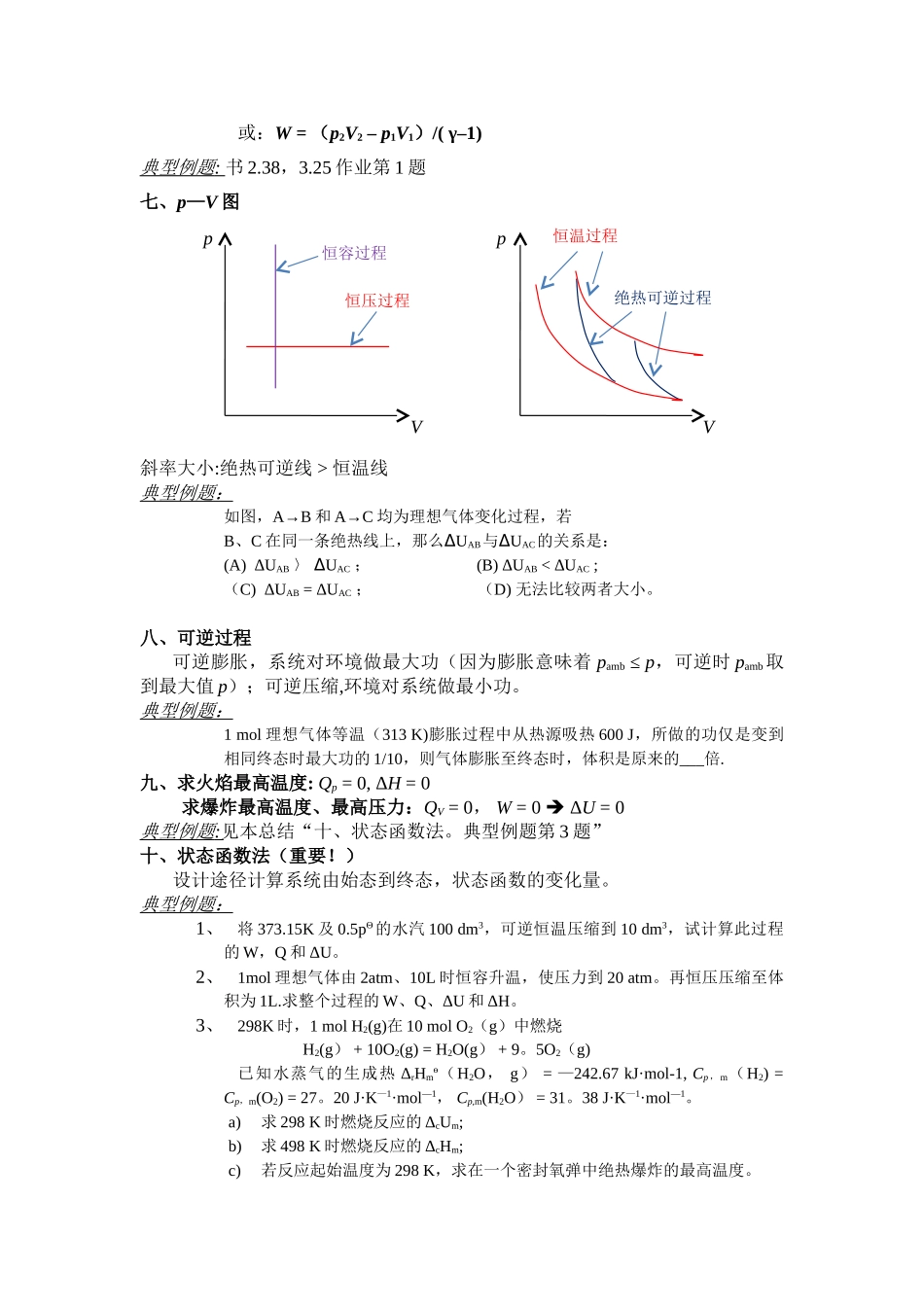
热一定律总结一、通用公式ΔU = Q + W绝热: Q = 0,ΔU = W恒容(W’=0):W = 0,ΔU = QV恒压(W’=0):W=—pΔV=—Δ(pV),ΔU = Q-Δ(pV) ΔH = Qp恒容+绝热(W’=0) :ΔU = 0恒压+绝热(W’=0) :ΔH = 0焓的定义式:H = U + pV ΔH = ΔU + Δ(pV)典型例题:3。11 思考题第 3 题,第 4 题。二、理想气体的单纯 pVT 变化恒温:ΔU = ΔH = 0变温: 或 或 如恒容,ΔU = Q,否则不一定相等。如恒压,ΔH = Q,否则不一定相等。Cp, m – CV, m = R双原子理想气体:Cp, m = 7R/2, CV, m = 5R/2单原子理想气体:Cp, m = 5R/2, CV, m = 3R/2典型例题 : 3.18 思考题第 2,3,4 题 书 2.18、2.19三、凝聚态物质的 ΔU 和 ΔH 只和温度有关或典型例题:书 2。15四、可逆相变(一定温度 T 和对应的 p 下的相变,是恒压过程)ΔU ≈ ΔH –ΔnRT(Δn:气体摩尔数的变化量。如凝聚态物质之间相变,如熔化、凝固、转晶等,则 Δn = 0,ΔU ≈ ΔH。101。325 kPa 及其对应温度下的相变可以查表.其它温度下的相变要设计状态函数ΔU = n CV, mdTT2T1∫ΔH = n Cp, mdTT2T1∫ΔU = nCV, m(T2-T1)ΔH = nCp, m(T2-T1)ΔU ≈ ΔH = n Cp, mdTT2T1∫ΔU ≈ ΔH = nCp, m(T2-T1)ΔH = Qp = nΔ Hmαβ不管是理想气体或凝聚态物质,ΔH1和 ΔH3均仅为温度的函数,可以直接用 Cp,m计算.或典型例题: 3 。 18 作业题第 3 题 五、化学反应焓的计算其他温度:状态函数法ΔU 和 ΔH 的关系:ΔU = ΔH –ΔnRT (Δn:气体摩尔数的变化量.)典型例题:3.25 思考题第 2 题典型例题:见本总结“十、状态函数法。典型例题第 3 题”六、体积功的计算通式:δW = —pamb·dV恒外压:W = -pamb·(V2—V1) 恒温可逆(可逆说明 pamb = p):W = nRT·ln(p2/p1) = —nRT·ln(V2/V1)绝热可逆:pVγ= 常数(γ = Cp, m/CV, m)。 利用此式求出末态温度 T2,则 W =ΔU = nCV, m(T2 – T1)Δ Hm(T) = ΔH1 +Δ Hm(T0) + ΔH3αββαΔ Hm(T)αβα 相,温度 T ,压力pα 相,温度 T0,压力 101.325 kPaΔH1β 相,温度 T ,压力pβ 相,温度 T0,压力 101.325 kPaΔH3Δ Hm(T0)αβ可逆相变298.15 K:稳定单质反应物aA + bBΔrHmө生成物yY + zZ完全燃烧产...