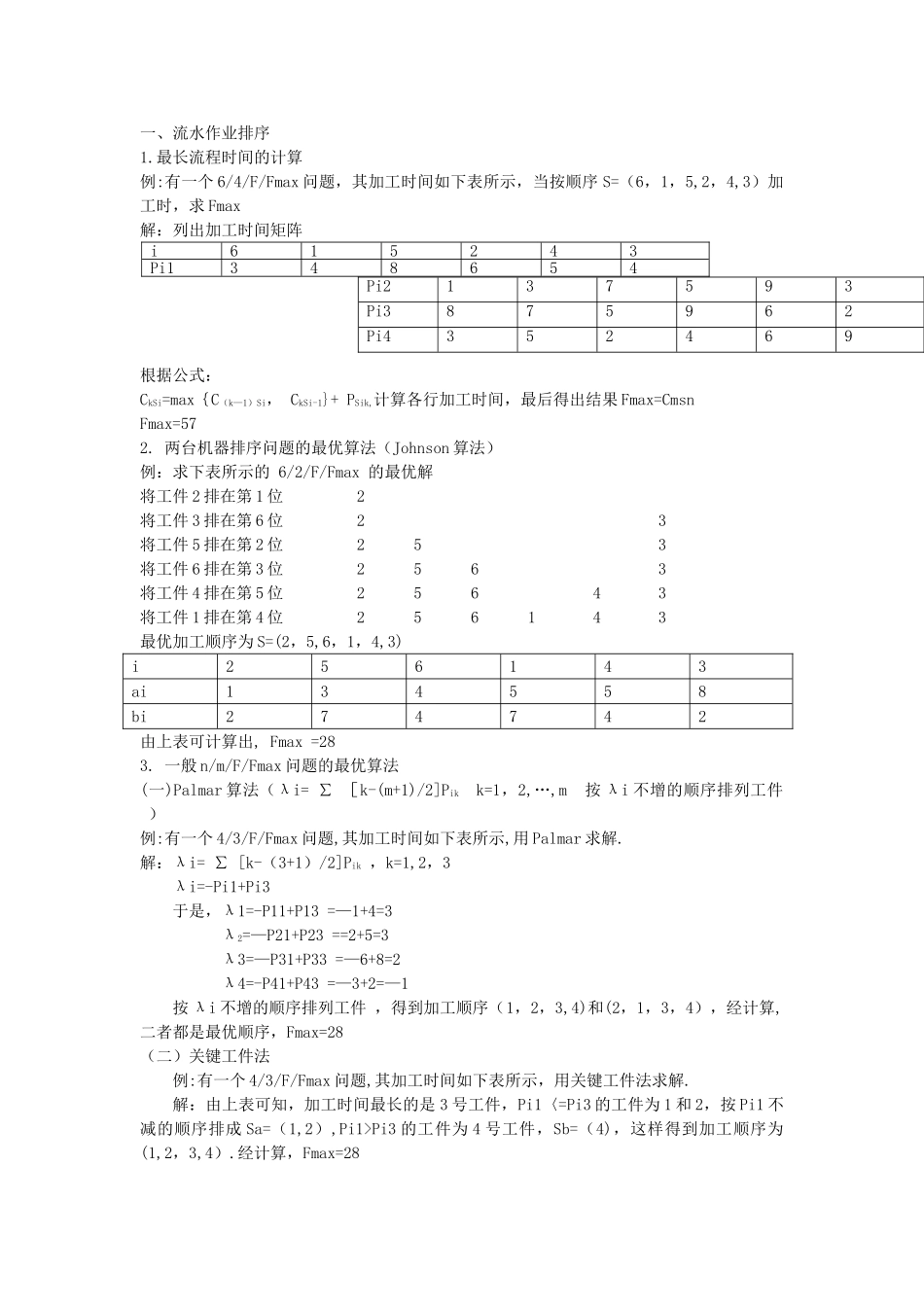
一、流水作业排序1.最长流程时间的计算例:有一个 6/4/F/Fmax 问题,其加工时间如下表所示,当按顺序 S=(6,1,5,2,4,3)加工时,求 Fmax解:列出加工时间矩阵根据公式:CkSi=max{C(k—1)Si, CkSi-1}+ PSik,计算各行加工时间,最后得出结果 Fmax=CmsnFmax=572. 两台机器排序问题的最优算法(Johnson 算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件 2 排在第 1 位 2将工件 3 排在第 6 位 2 3将工件 5 排在第 2 位 2 5 3将工件 6 排在第 3 位 2 5 6 3将工件 4 排在第 5 位 2 5 6 4 3将工件 1 排在第 4 位 2 5 6 1 4 3最优加工顺序为 S=(2,5,6,1,4,3)i256143ai134558bi274742由上表可计算出, Fmax =283. 一般 n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]Pik k=1,2,…,m 按 λi 不增的顺序排列工件 )例:有一个 4/3/F/Fmax 问题,其加工时间如下表所示,用 Palmar 求解.解:λi= ∑ [k-(3+1)/2]Pik ,k=1,2,3λi=-Pi1+Pi3 于是,λ1=-P11+P13 =—1+4=3 λ2=—P21+P23 ==2+5=3 λ3=—P31+P33 =—6+8=2 λ4=-P41+P43 =—3+2=—1按 λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28(二)关键工件法例:有一个 4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是 3 号工件,Pi1〈=Pi3 的工件为 1 和 2,按 Pi1 不减的顺序排成 Sa=(1,2),Pi1>Pi3 的工件为 4 号工件,Sb=(4),这样得到加工顺序为(1,2,3,4).经计算,Fmax=28i615243Pi1348654Pi2137593Pi3875962Pi4352469二、生产能力的计算(一)、对于加工装配式生产,生产能力是一个模糊的概念. 大量生产,品种单一,可用具体产品数表示; 大批生产,品种数少,可用代表产品数表示; 多品种、中小批量生产,则只能以假定产品(Pseudo-product)的产量来表示 。(二)、代表产品 适用于:产品结构、工艺相似、多品种生产的企业。选择其中劳动总量最大的一种作为代表产品,以代表产品产量表示生产能力. 换算步骤: ① 计算产量换算系数 Ki:i 产品产量换算系数 ti:i 产品台时定额 t 代:代表产品台时定额 ② 将 i 产品产量换算为代表产品产量 (三)、 假定产品:由各种产品按其总劳动量比重构成的一种假想产品 适用于:产品结构、工艺不相似,多...