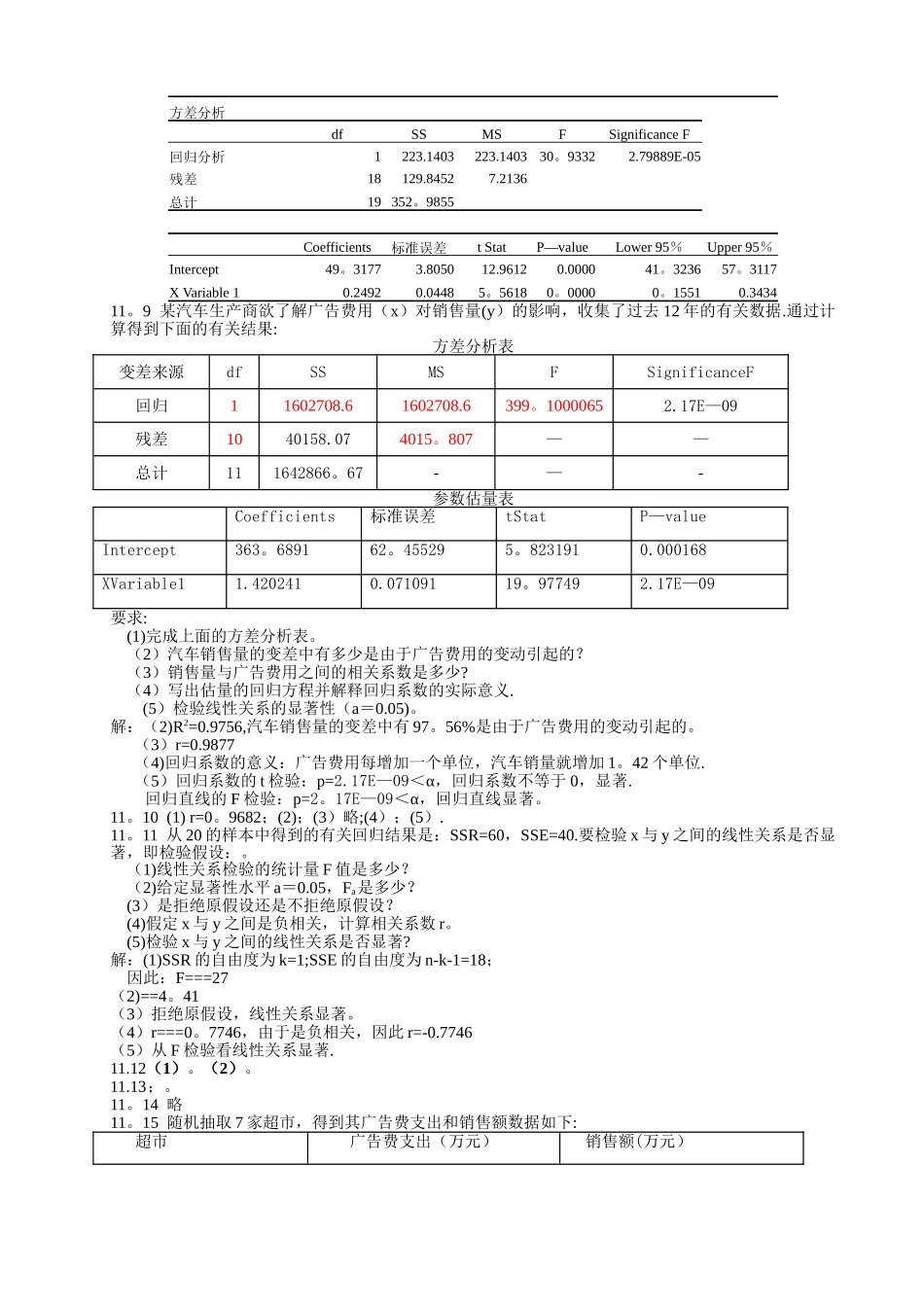
第 11 章 一元线性回归分析11.1(1)散点图(略),产量与生产费用之间正的线性相关关系.(2)(3)检验统计量,拒绝原假设,相关系数显著。11.2 (1)散点图(略)。11.3 (1)表示当时的期望值.(2)表示每变动一个单位平均下降 0.5 个单位。11.4 (1)(2)11。5 一家物流公司的管理人员想讨论货物的运输距离和运输时间的关系,为此,他抽出了公司最近10 个卡车运货记录的随机样本,得到运送距离(单位:km)和运送时间(单位:天)的数据如下:运送距离 x825 215 1070 550 480 920 1350 325 670 1215运送时间 y3.5 1.0 4。0 2.0 1。0 3。0 4。5 1.5 3.0 5。0要求:(1)绘制运送距离和运送时间的散点图,推断二者之间的关系形态:(2)计算线性相关系数,说明两个变量之间的关系强度。(3)利用最小二乘法求出估量的回归方程,并解释回归系数的实际意义。解:(1)可能存在线性关系。(2)相关性 x 运送距离(km)y 运送时间(天)x 运送距离(km)Pearson 相关性1.949(**)显著性(双侧) 0。000N1010y 运送时间(天)Pearson 相关性。949(**)1显著性(双侧)0.000 N1010**。 在 。01 水平(双侧)上显著相关。有很强的线性关系。(3)系数(a)模型 非标准化系数标准化系数t显著性B标准误Beta1(常量)0.1180.355 0。3330.748x 运送距离(km)0。0040。0000.9498。5090。000a. 因变量: y 运送时间(天)回归系数的含义:每公里增加 0。004 天。11。6 下面是 7 个地区 2000 年的人均国内生产总值(GDP)和人均消费水平的统计数据: 地区 人均 GDP(元) 人均消费水平(元) 北京 辽宁 上海 江西 河南 贵州 陕西 22 460 11 226 34 547 4 851 5 444 2 662 4 549 7 326 4 490 11 546 2 396 2 208 1 608 2 035要求: (1)人均 GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。 (2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。 (3)利用最小二乘法求出估量的回归方程,并解释回归系数的实际意义. (4)计算判定系数,并解释其意义。 (5)检验回归方程线性关系的显著性(a=0。05)。 (6)假如某地区的人均 GDP 为 5 000 元,预测其人均消费水平。 (7)求人均 GDP 为 5 000 元时,人均消费水平 95%的置信区间和预测区间。解:(1)__可能存在线性关系。(2)相关系数:相关性 人均 GDP(元)人均消费水平...