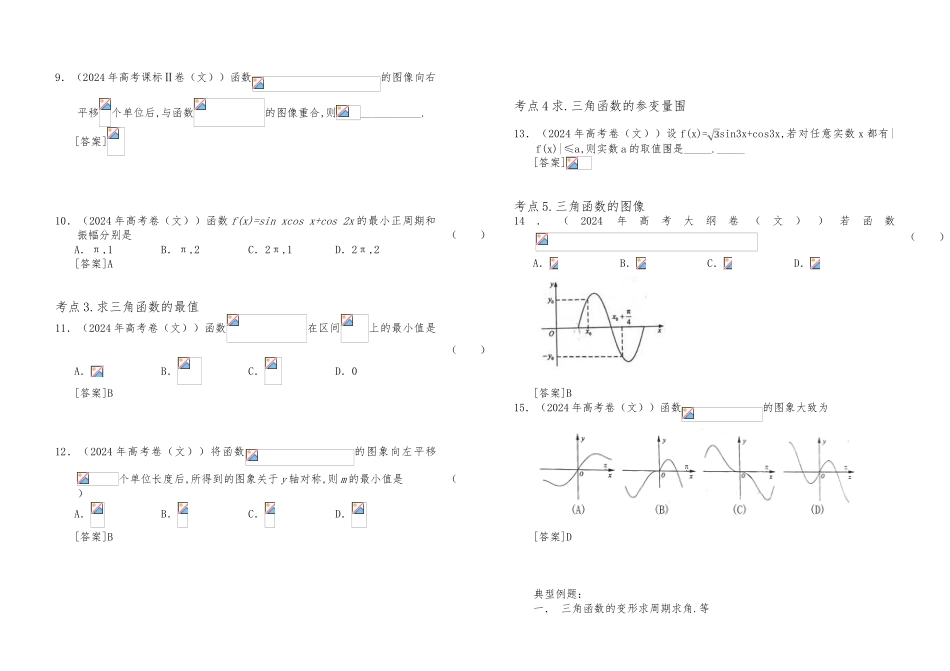
2024 年第二轮复习 三角函数的图像和性质 第 3 小时 (共 28 小时)高考总分 750 分,高考得分 723 分的高考状元龚杰同学的数学老师老师讲课(2024 年高考(文))已知函数 f(x)=(1) 求的值;(2) 求使成立的 x 的取值集合解: (1) .(2)由(1)知,在每一个区间(kπ-,kπ+)(k∈Z)内都是增函数递增区间[2kπ-π,2kπ]递减区间[2kπ,2kπ+π](k∈Z)递增区间[2kπ-,2kπ+]递减区间[2kπ+,2kπ+](k∈Z)单调性对称中心(kπ,0)(k∈Z)对称中心(kπ+,0)对称轴x=kπ(k∈Z)对称中心(kπ,0)对称轴x=kπ+(k∈Z)对称性奇函数偶函数奇函数奇偶性T=πT=2πT=2π周期性R[-1,1][-1,1]值域{x|x∈R,且x≠kπ+,k∈Z}RR定义域图象y=tanxy=cosxy=sinx12.基本公式 (1) 两角和差公式sin(α±β)=sinα·cosβ±cosα·sinβ;cos(α±β)=cosα·cosβ∓sinα·sinβ;tan(α±β)=.(2)二倍角公式sin2α=2sinαcosα;cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α;tan2α=.(3)辅助角公式asinα+bcosα=sin(α+φ)(其中 tanφ=).(4)常用公式变形 cos2α=;sin2α=.tanα±tanβ=tan(α±β)(1∓tanαtanβ).(5)诱导公式:分析:三角函数 2024 年全国各地高考文科数学考点 1.求三角函数值1 .(2024 年高考大纲卷(文))已知是第二象限角,( )A.B.C.D.2 .(2024 年高考卷(文))( )A.B.C.D.[答案]C 3.(2024 年高考课标Ⅱ卷(文))已知 sin2α= ,则 cos2(α+ )=( )A.B.C.D.[答案]A4.(2024 年高考卷(文))已知,那么( )A.B.C.D.[答案]C 5.(2024 年高考卷(文))设,,则的值是________.[答案]6 . ( 2024 年 高 考 数 学 试 题 ( 文 科 ) ) 若, 则________. [答案]7.(2024 年高考课标Ⅰ卷(文))设当时,函数取得最大值,则______.[答案];考点 2.求三角函数有关参变量值8 .(2024 年高考卷(文))将函数的图象向右平移个单位长度后得到函数的图象,若的图象都经过点,则的值可以是( )A.B.C.D.[答案]B 9.(2024 年高考课标Ⅱ卷(文))函数的图像向右平移个单位后,与函数的图像重合,则___________.[答案]10.(2024 年高考卷(文))函数 f(x)=sin xcos x+cos 2x 的最小正周期和振幅分别是( )A.π,1B.π,2C.2π,1D.2π,2[答案]A 考点 3.求三角函数的最值11.(2024 年高考卷(文))函数在区...