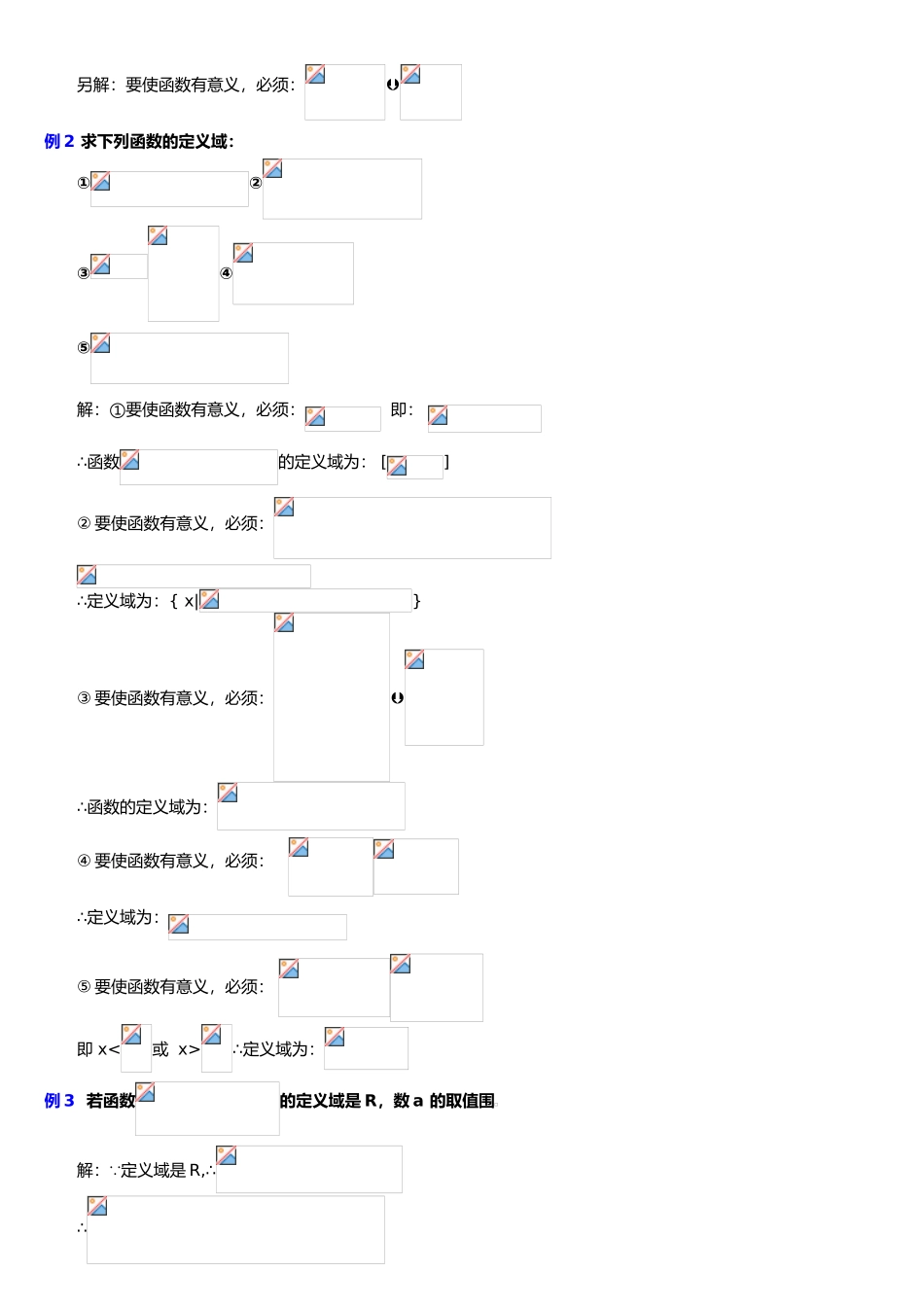
函数定义域、值域求法总结一、定义域是函数中的自变量 x 的围。求函数的定义域需要从这几个方面入手: (1)分母不为零 (2)偶次根式的被开方数非负。(3)对数中的真数部分大于 0。 (4)指数、对数的底数大于 0,且不等于 1 (5)y=tanx 中 x≠kπ+π/2;y=cotx 中 x≠kπ 等等。( 6 )中 x二、值域是函数中 y 的取值围。 常用的求值域的方法: (1)直接法 (2)图象法(数形结合) (3)函数单调性法(4)配方法 (5)换元法 (包括三角换元) (6)反函数法(逆求法) (7)分离常数法 (8)判别式法 (9)复合函数法(10)不等式法 (11)平方法等等这些解题思想与方法贯穿了高中数学的始终。三、典例解析1、定义域问题例 1 求下列函数的定义域:①;②;③解:① x-2=0,即 x=2 时,分式无意义,而时,分式有意义,∴这个函数的定义域是.② 3x+2<0,即 x<-时,根式无意义,而,即时,根式才有意义,∴这个函数的定义域是{|}.③ 当,即且时,根式和分式 同时有意义,∴这个函数的定义域是{|且}另解:要使函数有意义,必须:例 2 求下列函数的定义域:①②③④⑤解:①要使函数有意义,必须: 即: ∴函数的定义域为: []② 要使函数有意义,必须:∴定义域为:{ x|}③ 要使函数有意义,必须:∴函数的定义域为:④ 要使函数有意义,必须: ∴定义域为:⑤ 要使函数有意义,必须: 即 x<或 x>∴定义域为:例 3 若函数的定义域是 R,数 a 的取值围解: 定义域是 R,∴∴例 4 若函数的定义域为[1,1],求函数的定义域解:要使函数有意义,必须:∴函数的定义域为:例 5 已知 f(x)的定义域为[-1,1],求 f(2x-1)的定义域。分析:法则 f 要求自变量在[-1,1]取值,则法则作用在 2x-1 上必也要求 2x-1 在 [-1,1]取值,即-1≤2x-1≤1,解出 x 的取值围就是复合函数的定义域;或者从位置上思考 f(2x-1)中 2x-1 与 f(x)中的 x 位置一样,围也应一样,∴-1≤2x-1≤1,解出 x 的取值围就是复合函数的定义域。(注意:f(x)中的 x 与 f(2x-1)中的 x 不是同一个 x,即它们意义不同。)解: f(x)的定义域为[-1,1],∴-1≤2x-1≤1,解之 0≤x≤1,∴f(2x-1)的定义域为[0,1]。例 6 已知已知 f(x)的定义域为[-1,1],求 f(x2)的定义域。答案:-1≤x2≤1 x2≤1-1≤x≤1练习:设的定义域是[3,],求函数的定义域解:要使函数有意...