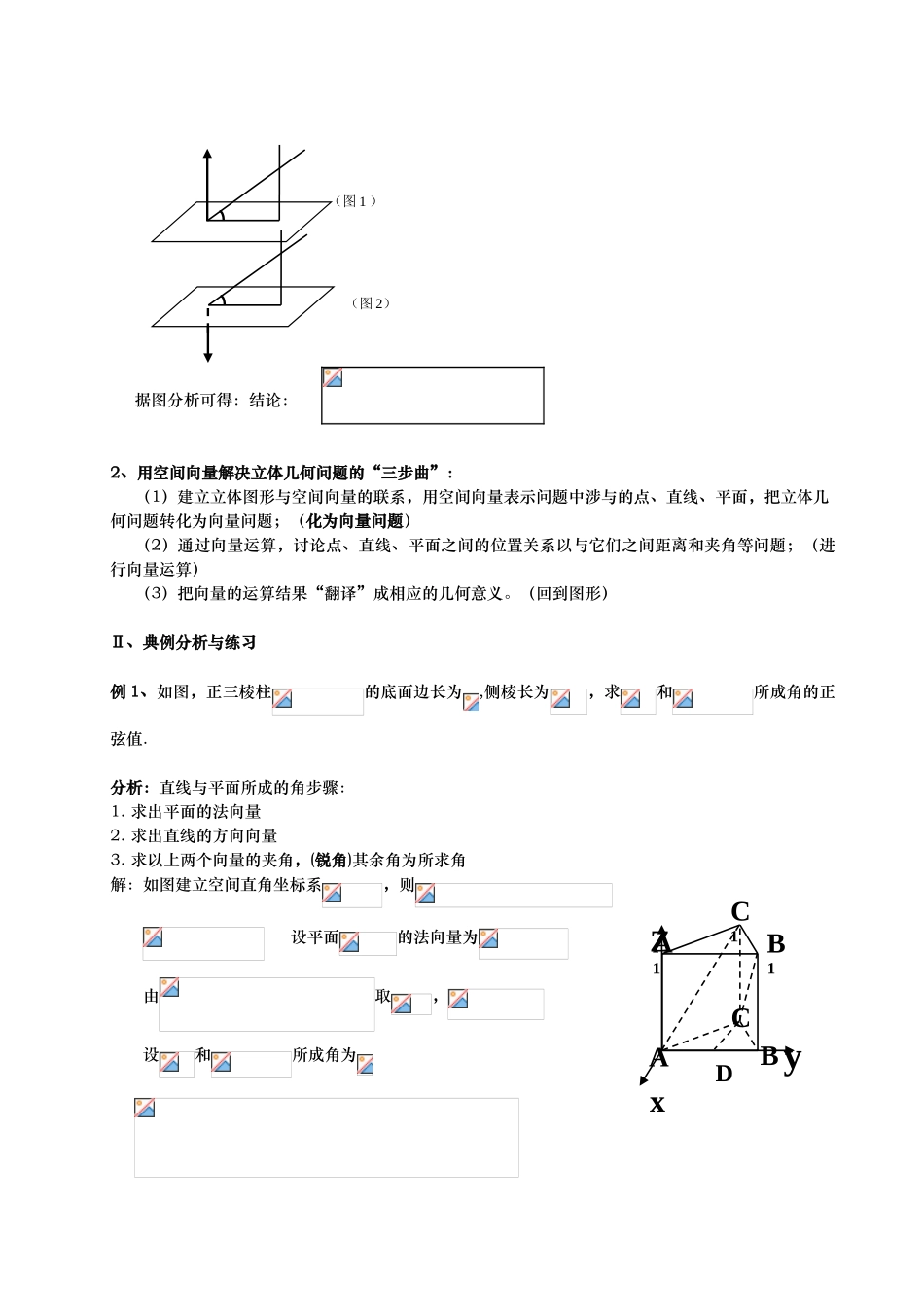
第二讲:立体几何中的向量方法——利用空间向量求直线与平面所成的角大家知道,立体几何是高中数学学习的一个难点,以往学生学习立体几何时,主要实行“形到形”的综合推理方法,即根据题设条件,将空间图形转化为平面图形,再由线线,线面等关系确定结果,这种方法没有一般规律可循,对人的智力形成极大的挑战,技巧性较强,致使大多数学生都感到束手无策。高中新教材中,向量知识的引入,为学生解决立体几何问题提供了一个有效的工具。它能利用代数方法解决立体几何问题,体现了数形结合的思想。并且引入向量,对于某些立体几何问题提供通法 ,避开了传统立体几何中的技巧性问题,因此降低了学生学习的难度,减轻了学生学习的负担,体现了新课程理念。为适应高中数学教材改革的需要,需要讨论用向量法解决立体几何的各种问题。本文举例说明如何用向量法解决立体几何的空间角问题。以此强化向量的应用价值,激发学生学习向量的兴趣,从而达到提高学生解题能力的目的。利用向量法求空间角,不需要繁杂的推理,只需要将几何问题转化为向量的代数运算,方便快捷。空间角主要包括线线角、线面角和二面角,下面对线面角的求法进行总结。教学目标1.使学生学会求平面的法向量与直线与平面所成的角的向量方法;2.使学生能够应用向量方法解决一些简单的立体几何问题;3.使学生的分析与推理能力和空间想象能力得到提高.教学重点求平面的法向量;求解直线与平面所成的角的向量法.教学难点 求解直线与平面所成的角的向量法.教学过程Ⅰ、复习回顾一、回顾有关知识:1、直线与平面所成的角:(X 围:)思考:设平面的法向量为,则与的关系?ABCA1B1C1xyZD据图分析可得:结论:2、用空间向量解决立体几何问题的“三步曲”:(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉与的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题)(2)通过向量运算,讨论点、直线、平面之间的位置关系以与它们之间距离和夹角等问题;(进行向量运算)(3)把向量的运算结果“翻译”成相应的几何意义。(回到图形)Ⅱ、典例分析与练习例 1、如图,正三棱柱的底面边长为,侧棱长为,求和所成角的正弦值.分析:直线与平面所成的角步骤: 1. 求出平面的法向量2. 求出直线的方向向量3. 求以上两个向量的夹角,(锐角)其余角为所求角解:如图建立空间直角坐标系,则 设平面的法向量为由取,设和所成角为(图 1 )(图 2)和所成角的正弦值.点拨 要...