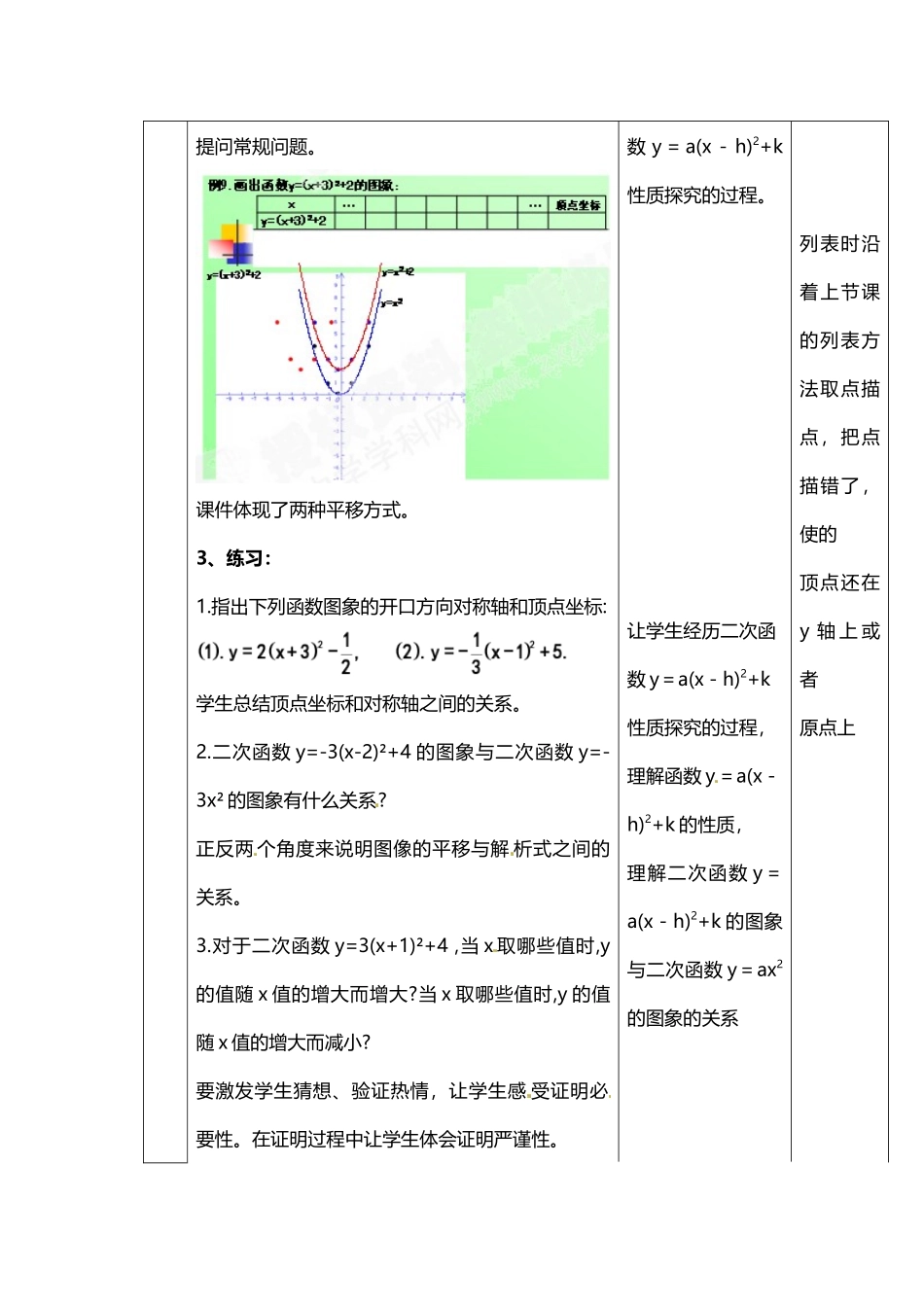
第 3 课时 二次函数 y=a(x-h)2+k 的图象和性质教材分析之前学生已经学过一次函数、反比例函数的图像和性质,以及会建立二次函数的模型和理解二次函数的图像相关概念和性质基础之上进行的。是前面知识的应用和拓展,又为今后学习二次函数的应用及一元二次方程与二次函数之间的关系作预备。充分体现了数形结合的思想,因此本课无论在知识上还是培育学生动手能力上都起了很大的作用。学生已经会了上一节的二次函数图像及性质。课标要求会用描点法画出二次函数的图像,通过图像了解二次函数的性质。学情分析可能有些学生对二次函数还不理解,甚至还不会描点法画出函数图像,看图能力差,不能类比一次函数的一些观察图像的方法来学习二次函数的图像。不能从图中猎取相关的信息。由于放假的原因,学生对上下平移和 左右平移的知识有很多忘却,所以完成本节知识在理解方面会有难点。教学目标[来源:Z#xx知识目标:让学生经历二次函数 y=a(x-h)2+k 性质探究的过程,理解函数 y=a(x-h)2+k 的性质,理解二次函数 y=a(x-h)2+k 的图象与二次函数 y=ax2的图象的关系[来源:Z|xx|k.Com][来源:学科网][来源:Zxxk.Com]能力目标:通过画图象独立去探究沟通图象的性质培育分析解决问题的能力。能说出二次函数 y=a(x-h)2+k 的图象与二次函数 y=ax2的图象的关系。情意目标:在学习中体会知识之间的联系,体会知识的发生进展过程和知识体系。教学重点:会用描点法画出二次函数 y=a(x-h)2+k 的图象,理解二次函数 y=a(x-h)2+k 的性质。能说出顶点坐标。#k.Co教学难点:理解二次函数 y=a(x-h)2+k 的性质,理解二次函数 y=a(x-h)2+k 的图象与二次函数 y=ax2关系。教学手段 导学案教学方法 问答法、练习法、讨论法教学过程1、创设情境::(组织方法)复习两个上下平移及左右平移的二次数学图像 ,对比图像说出开口方向、对称轴、顶点坐标、最值、性质。详见导学案。解 决 哪 些 教 学 目标:在学习中体会知识之间的联系,体会知识的发生进展过程和知识体系。学生可能出现的困难:忘记或混淆上下平移和左右平移。2、新授(1):(课件辅助)直接提问上下和左右平移的例子,由特别到一般,解 决 哪 些 教 学 目标:让学生经历二次函学生可能出现的困难:提问常规问题。课件体现了两种平移方式。3、练习:1.指出下列函数图象的开口方向对称轴和顶点坐标: 学生总结顶点坐标和对称轴之间的关系。2.二次函数 y=-3(x-...